クレーン・デリック運転士過去問
令和7年（2025年）4月
問2 (クレーン及びデリックに関する知識問2)

問題文

図において、電動機の回転軸に固定された歯車Aが電動機の駆動により毎分1600回転し、これにかみ合う歯車の回転により、歯車Dが毎分80回転しているとき、歯車Cの歯数の値として、正しいものは次のうちどれか。
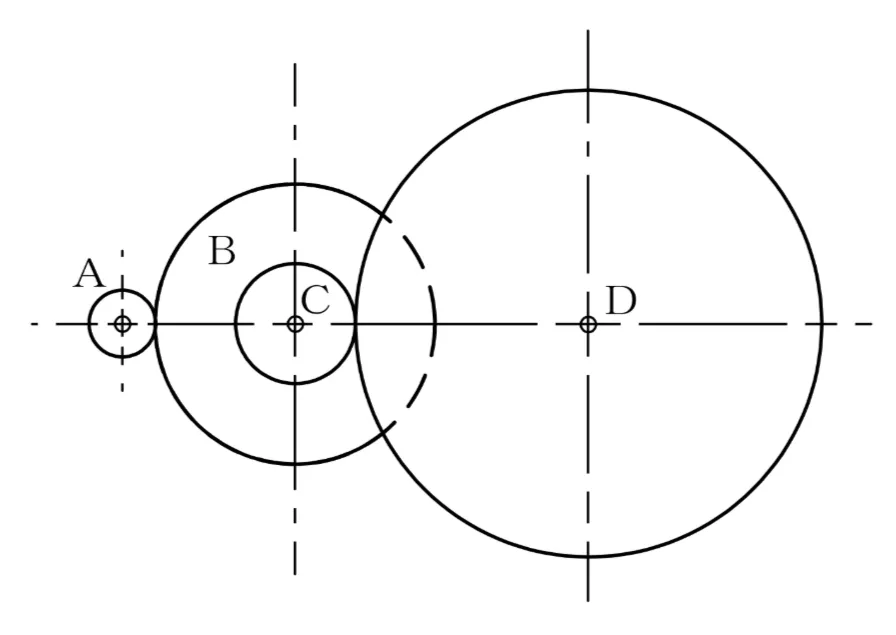
ただし、歯車A、B及びDの歯数は、それぞれ16枚、64枚及び120枚とし、BとCの歯車は同じ軸に固定されているものとする。問題文の画像

付箋

イエロー
グリーン
ブルー
レッド

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

クレーン・デリック運転士試験令和7年（2025年）4月問2（クレーン及びデリックに関する知識問2）（訂正依頼・報告はこちら）

21枚
24枚
28枚
30枚
32枚

次の問題へ

正解！素晴らしいです

残念...

この過去問の解説（2件）

この問題は複合歯車列の回転比を扱います。
ポイントは2つです。

同軸で固定された歯車同士（ここではBとC）は回転数が同じです。

かみ合う2枚の外歯車の回転数比は歯数の逆比（例：A→Bなら n_B＝n_A×Z_A÷Z_B）です。
この2つを順に掛け合わせるだけで求められます。

選択肢1. 21枚

誤りです。
21では計算が合いません。

選択肢2. 24枚

正しいです。
計算手順を示します（n＝回転数、Z＝歯数）
A→B：n_B＝1600×16÷64＝400 rpm
BとCは同軸：n_C＝n_B＝400 rpm
C→D：n_D＝n_C×Z_C÷120＝400×Z_C÷120
与えられた n_D＝80 なので、80＝400×Z_C÷120 → Z_C＝24。

選択肢3. 28枚

誤りです。
Z_C＝28を代入すると
n_D＝400×28÷120＝93.3… rpm。80になりません。

選択肢4. 30枚

誤りです。
n_D＝400×30÷120＝100 rpm。80になりません。

選択肢5. 32枚

誤りです。
n_D＝400×32÷120＝106.6… rpm。80になりません。

まとめ

同軸固定＝回転数同じ、かみ合い＝歯数の逆比を落ち着いて適用します。

複合列では段ごとに比を掛け合わせ、最後に与えられた回転数に合わせて未知の歯数を解きます。

計算量自体は多くないため、比の考え方ができれば確実に得点できます。

参考になった数2

この解説の修正を提案する

次の問題は下へ

速度伝達比の問題です。一見難しそうに感じますが、ポイントとしては各歯車がどのように回転するか見極める事が重要です。

選択肢2. 24枚

図のような二段減速の伝達比は、大きい歯車÷小さい歯車で求めます。2つあるので、それぞれ掛けたものが伝達比と等しくなります。したがって、Ｂ÷A×Ｄ÷Ｃとなるので、

1,600×80＝64÷16×120÷Ｃ

このような式となり、この式を解くと

Ｃ＝24枚となるので、この選択肢の値が適切となります。

まとめ

解き方さえ分かればすぐに解ける問題なので、この解き方は覚えておきましょう。

参考になった数3

この解説の修正を提案する

（訂正依頼・報告はこちら）

クレーン・デリック運転士 過去問 令和7年（2025年）4月 問2 (クレーン及びデリックに関する知識 問2)

問題

この過去問の解説 （2件）

クレーン・デリック運転士過去問
令和7年（2025年）4月
問2 (クレーン及びデリックに関する知識問2)

この過去問の解説（2件）