クレーン・デリック運転士 過去問
令和7年（2025年）4月
問22 (原動機及び電気に関する知識 問2)
問題文
図のような回路について、AE間に60Vの電圧をかけたときの電流I（A）、電圧E（V）、抵抗R（Ω）の値に関する記述として、適切でないものは次のうちどれか。 
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
クレーン・デリック運転士試験 令和7年（2025年）4月 問22（原動機及び電気に関する知識 問2） （訂正依頼・報告はこちら）
図のような回路について、AE間に60Vの電圧をかけたときの電流I（A）、電圧E（V）、抵抗R（Ω）の値に関する記述として、適切でないものは次のうちどれか。
- AB間の電圧の値は48Ⅴである。
- BC間の電圧の値は12Ⅴである。
- AE間の抵抗の値は10Ωである。
- B点を流れる電流の値は6Aである。
- D点を流れる電流の値は4Aである。
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
電流、電圧、抵抗に関する問題です。この問題を解くポイントは合成抵抗を正しく解けるかが重要となっています。
ＢＥ間の合成抵抗は「和分の積」で求めます。それぞれ代入すると
（3×6）÷（3+6）＝2Ω
これで直流回路となるのでAE間の合成抵抗は
8+2＝10Ω
それぞれに係る電圧を求めると
AＢ間の電圧は
60×8÷10＝48Ｖ
ＢＣ間の電圧は
60×2÷10＝12Ｖ
最後に電流値を求めると
Ｂの電流値は
48÷8＝6A
Ｄの電流値は
12÷6＝2A
したがってこの選択肢の値が不適切となります。
合成抵抗の求め方以外にも電流電圧抵抗の公式も忘れないようにしましょう。
参考になった数5
この解説の修正を提案する
02
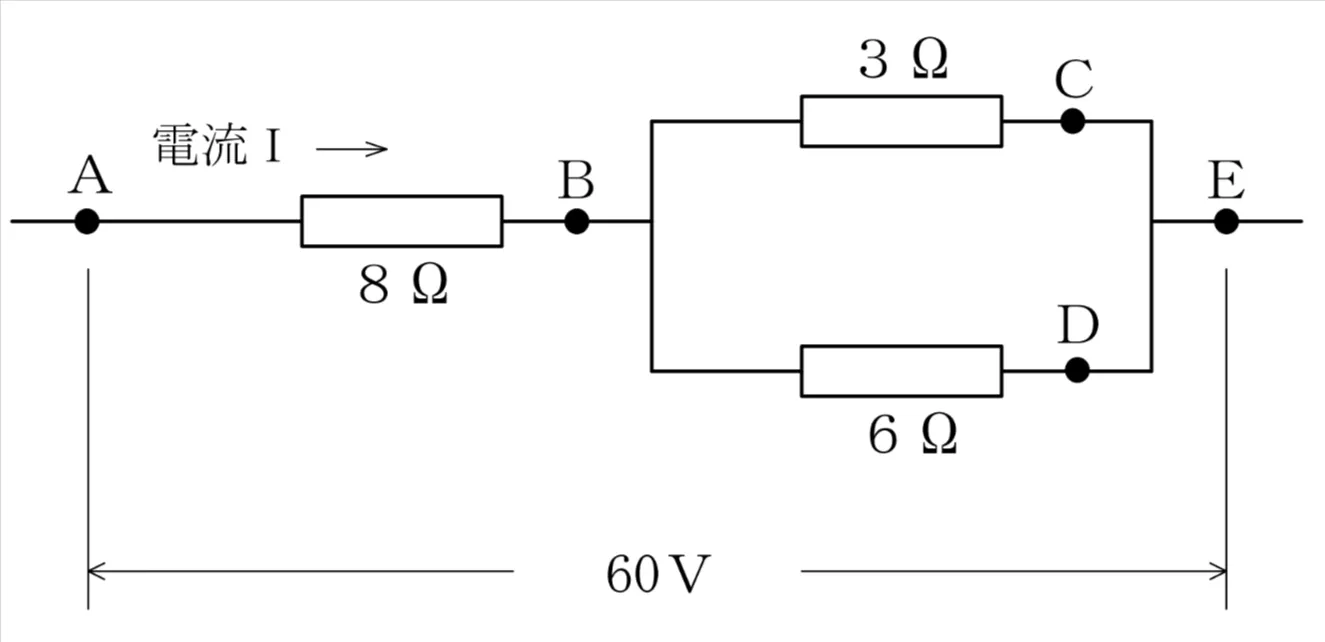
図は、A−B間に8Ω、その先で3Ωと6Ωが並列、右端で再び一点にまとまりEへ至る直並列回路です。
手順は、並列部の合成抵抗を求める→全体抵抗→全電流I→各部の電圧と枝電流、の順で確実に計算します。
並列部は3Ωと6Ωの和9に対して積18を用い、18 ÷ 9 ＝ 2Ωとなります。直列合成は8Ωと2Ωの合計で10Ωです。
よって全電流Iは60 ÷ 10 ＝ 6A、並列部にかかる電圧はI × 2 ＝ 12Vです。
正しいです。
AB間の電圧は全電流6Aが8Ωを流れるので6 × 8 ＝ 48Vです。
正しいです。
BC間は並列上側の3Ωにかかる電圧で、並列部の電圧と同じです。並列部の電圧はI × 2 ＝ 12Vなので、BC間も12Vです。
正しいです。
AE間の抵抗は、並列部2Ωと8Ωの直列合成で10Ωです。
正しいです。
B点を通る電流は全電流Iです。I ＝ 60 ÷ 10 ＝ 6Aです。
誤りです。
D点（下側枝）の電流は並列部の電圧12Vが6Ωにかかるので12 ÷ 6 ＝ 2Aです。4Aではありません。
直並列の合成を先に固め、全電流Iを出してから各部の電圧と枝電流を求めると、計算ミスを防げます。
とくに、並列の合成は積18と和9を使って18 ÷ 9 ＝ 2Ωにする流れを癖にすると安定します。
参考になった数0
この解説の修正を提案する
前の問題（問21）へ
令和7年（2025年）4月 問題一覧
次の問題（問23）へ