2級管工事施工管理技士 過去問
令和7年度（2025年）前期
問30 (ユニットD 問2)
問題文
下図に示すネットワーク工程表に関する記述のうち、適当でないものはどれか。
ただし、図中のイベント間のA〜Hは作業内容、日数は作業日数を表す。
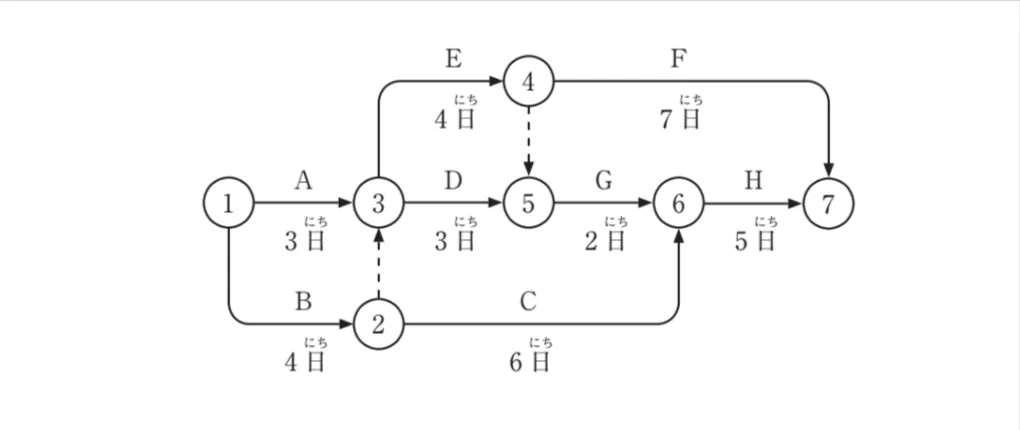
ただし、図中のイベント間のA〜Hは作業内容、日数は作業日数を表す。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
2級管工事施工管理技士試験 令和7年度（2025年）前期 問30（ユニットD 問2） （訂正依頼・報告はこちら）
下図に示すネットワーク工程表に関する記述のうち、適当でないものはどれか。
ただし、図中のイベント間のA〜Hは作業内容、日数は作業日数を表す。
ただし、図中のイベント間のA〜Hは作業内容、日数は作業日数を表す。
- クリティカルパスは3本で、所要日数は15日である。
- 作業Hの所要日数を1日短縮できると、全体の所要日数も1日短縮することができる。
- 作業A、Bは作業Dが開始される前に終了していなければならない。
- ②―③間や④―⑤間のような作業の相互関係だけを示す点線矢印をダミーという。
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問29）へ
令和7年度（2025年）前期 問題一覧
次の問題（問31）へ