大学入学共通テスト（数学） 過去問
令和4年度（2022年度）本試験
問80 (数学Ⅱ・数学B（第2問） 問8)
問題文
以下（ サ ），（ シス ）に当てはまるものを選べ。
〔2〕b＞0とし、g（x）＝x3－3bx＋3b2，h（x）＝x3－x2＋b2とおく。座標平面上の曲線y＝g（x）をC1，曲線y＝h（x）をC2とする。
C1とC2は2点で交わる。これらの交点のx座標をそれぞれα，β（α＜β）とすると、α＝（ サ ），β＝（ シス ）である。
α≦x≦βの範囲でC1とC2で囲まれた図形の面積をSとする。また、t＞βとし、β≦x≦tの範囲でC1とC2および直線x＝tで囲まれた図形の面積をTとする。
〔2〕b＞0とし、g（x）＝x3－3bx＋3b2，h（x）＝x3－x2＋b2とおく。座標平面上の曲線y＝g（x）をC1，曲線y＝h（x）をC2とする。
C1とC2は2点で交わる。これらの交点のx座標をそれぞれα，β（α＜β）とすると、α＝（ サ ），β＝（ シス ）である。
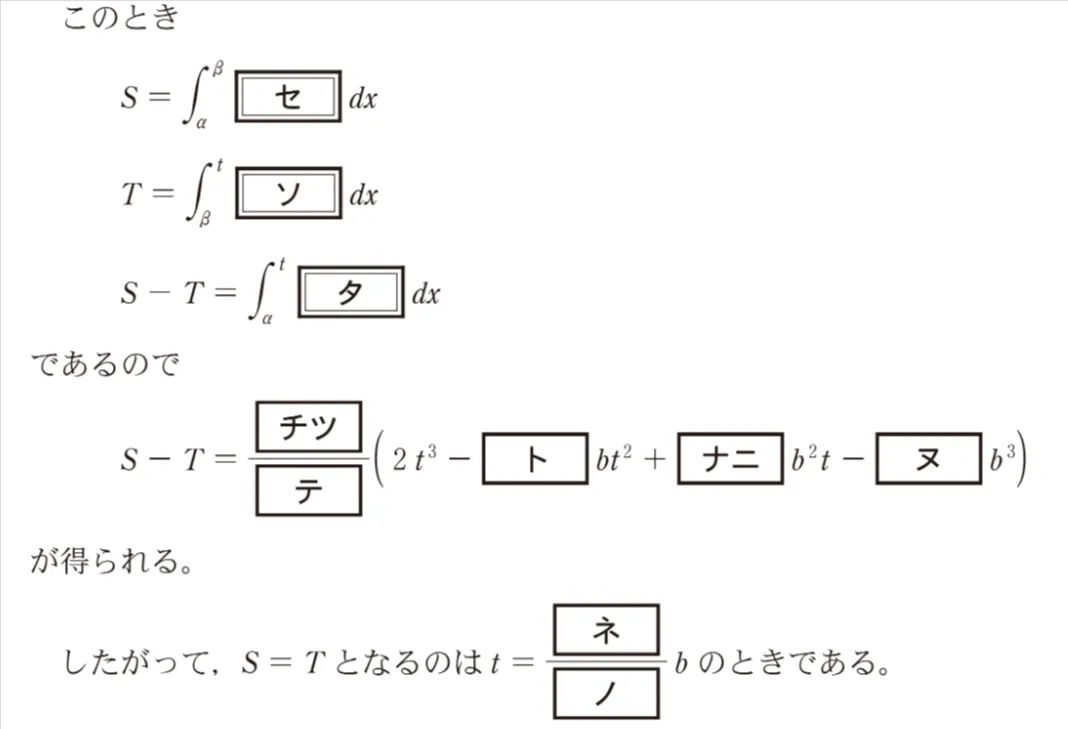
α≦x≦βの範囲でC1とC2で囲まれた図形の面積をSとする。また、t＞βとし、β≦x≦tの範囲でC1とC2および直線x＝tで囲まれた図形の面積をTとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）本試験 問80（数学Ⅱ・数学B（第2問） 問8） （訂正依頼・報告はこちら）
以下（ サ ），（ シス ）に当てはまるものを選べ。
〔2〕b＞0とし、g（x）＝x3－3bx＋3b2，h（x）＝x3－x2＋b2とおく。座標平面上の曲線y＝g（x）をC1，曲線y＝h（x）をC2とする。
C1とC2は2点で交わる。これらの交点のx座標をそれぞれα，β（α＜β）とすると、α＝（ サ ），β＝（ シス ）である。
α≦x≦βの範囲でC1とC2で囲まれた図形の面積をSとする。また、t＞βとし、β≦x≦tの範囲でC1とC2および直線x＝tで囲まれた図形の面積をTとする。
〔2〕b＞0とし、g（x）＝x3－3bx＋3b2，h（x）＝x3－x2＋b2とおく。座標平面上の曲線y＝g（x）をC1，曲線y＝h（x）をC2とする。
C1とC2は2点で交わる。これらの交点のx座標をそれぞれα，β（α＜β）とすると、α＝（ サ ），β＝（ シス ）である。
α≦x≦βの範囲でC1とC2で囲まれた図形の面積をSとする。また、t＞βとし、β≦x≦tの範囲でC1とC2および直線x＝tで囲まれた図形の面積をTとする。
- サ：x シス：3x
- サ：b シス：3b
- サ：x シス：2x
- サ：b シス：2b
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問79）へ
令和4年度（2022年度）本試験 問題一覧
次の問題（問81）へ