大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問103 (数学Ⅱ・数学B(第4問) 問10)
問題文
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
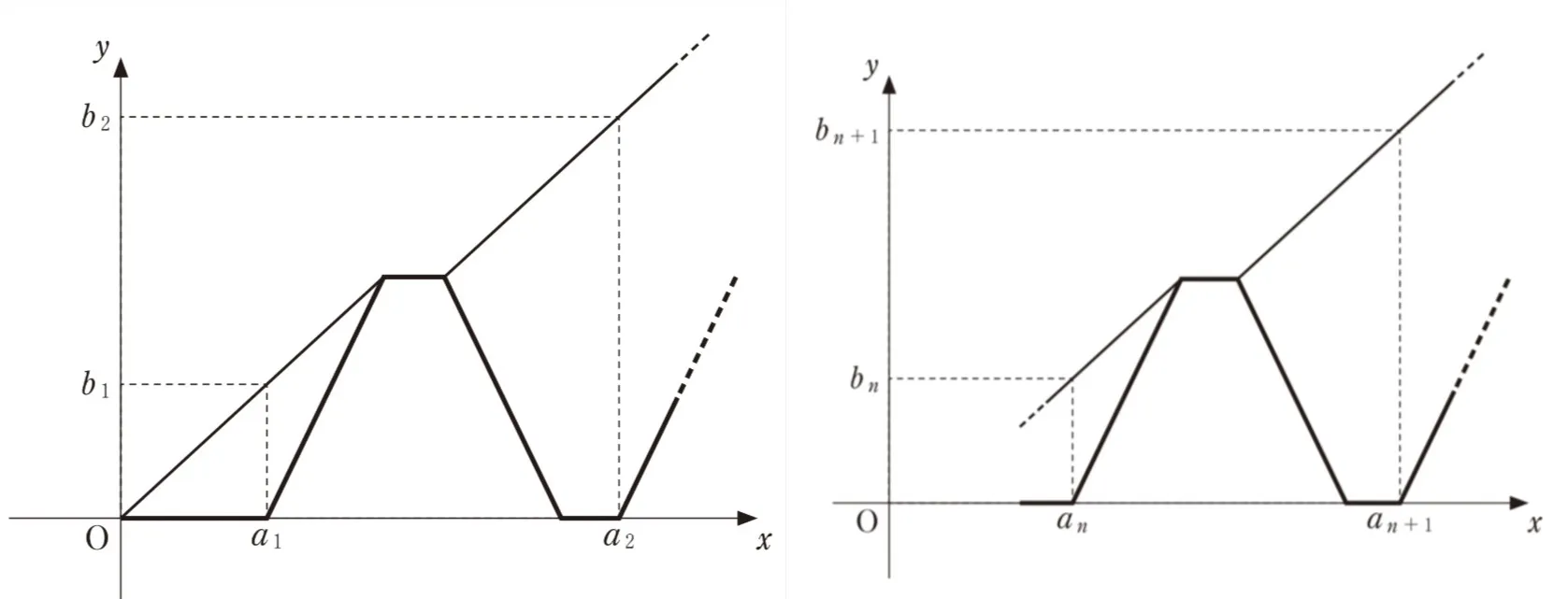
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標がyであるとき、その点は位置yにあるということにする。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
x=anを自転車がn回目に自宅を出発する時刻とし、y=bnをそのときの歩行者の位置とする。
(2)歩行者がy=300の位置に到着するときまでに、自転車が歩行者に追いつく回数は( サ )回である。また、( サ )回目に自転車が歩行者に追いつく時刻は、x=( シスセ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問103(数学Ⅱ・数学B(第4問) 問10) (訂正依頼・報告はこちら)
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標がyであるとき、その点は位置yにあるということにする。また、歩行者が自宅を出発してからx分経過した時点を時刻xと表す。歩行者は時刻0に自宅を出発し、正の向きに毎分1の速さで歩き始める。自転車は時刻2に自宅を出発し、毎分2の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分1の速さで歩き出し、自転車は毎分2の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分2の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
x=anを自転車がn回目に自宅を出発する時刻とし、y=bnをそのときの歩行者の位置とする。
(2)歩行者がy=300の位置に到着するときまでに、自転車が歩行者に追いつく回数は( サ )回である。また、( サ )回目に自転車が歩行者に追いつく時刻は、x=( シスセ )である。

- 1
- 2
- 3
- 4
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問102)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問104)へ