大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問141 (情報関係基礎(第2問) 問5)
問題文
次の文章を読み、空欄[ オ ]に最も適当なものを、後の解答群のうちから一つ選べ。
小池さんは、皆にも文字列の幸いさに親しんでもらいたいと思っている。文字列の幸いさを機械的に計算するために、まずは文字列に現れるすべての回文を求める方法を考えた。以下では「しばししばまた」を例に考える。
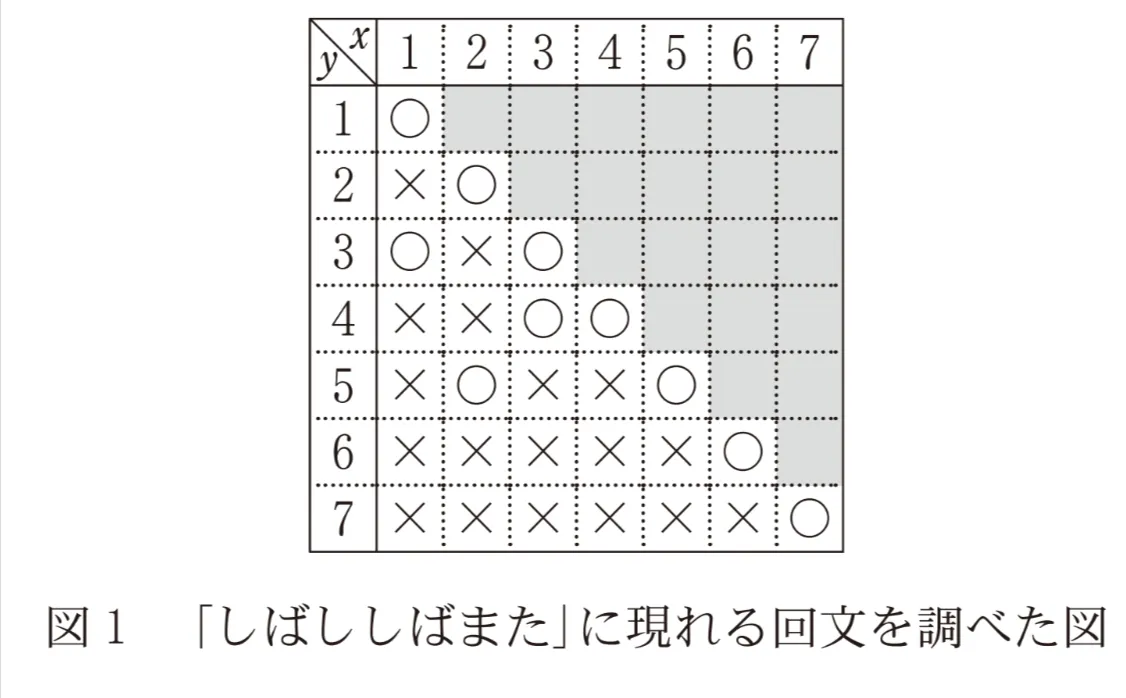
「しばししばまた」の中には1文字のもの以外には「しばし」や「しし」という回文があるが、回文を見落とすことがないように、次の図1を用いて文字列のx文字目からy文字目までが回文かどうかをすべてのx,yの組(ただし1≦x≦y≦7)について調べる。例えば(x,y)=(1,2)は文字列「しば」に対応し、これは回文ではない。回文「しし」は(x,y)=(3,4)に対応する。また、回文「ばししば」は(x,y)=([ オ ],[ カ ])に対応する。回文に対応するマスに〇,そうでないマスに✕を記入することですべての回文が求められる。
小池さんは図1を作る際に、長い文字列に対応するマスでも〇✕を決めるために調べる文字が少なくて済む、次の方法を考えた。
まず、長さ1の文字列は回文であるため、これに対応する図1の対角線上のマス(i,i)(ただし1≦i≦7)はすべて〇となる。また、長さ2の文字列は、マス(i,i+1)(ただし1≦i≦6)に対応するが、これはそれぞれの2文字を調べることで回文かどうかを判断し、マスの〇✕を決める。
残りのマスの〇✕を決めるためには、図1において✕の左下のマスは必ず✕であるという性質を利用する。これは、
x文字目からy文字目までが回文でないとき、その両隣のx-1文字目とy+1文字目がどのような文字であっても、x-1文字目からy+1文字目までは回文にはならない
からである。一方で、
x文字目からy文字目までが回文のとき、その両隣のx-1文字目とy+1文字目が( キ )ならば、x-1文字目からy+1文字目までは回文となり、そうでないならば回文にはならない
こともわかる。
このことを使い、長さ1と2の文字列に対応するそれぞれのマスから始めて順に左下のマスの〇✕を決めていく。例えば、(x,y)=(4,4)から始めると、このマスは〇なので次は([ ク ],[ ケ ])のマスの〇✕を考える。[ ク ]文字目と[ ケ ]文字目を調べ、✕と決められる。すると、(2,[ コ ])のマス、(1,[ サ ])のマスは、それ以上文字を調べずに✕と決められる。
この方法で図1を作成するとき、文字を調べずに✕と決めるマスは全部で( シ )個である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問141(情報関係基礎(第2問) 問5) (訂正依頼・報告はこちら)
次の文章を読み、空欄[ オ ]に最も適当なものを、後の解答群のうちから一つ選べ。
小池さんは、皆にも文字列の幸いさに親しんでもらいたいと思っている。文字列の幸いさを機械的に計算するために、まずは文字列に現れるすべての回文を求める方法を考えた。以下では「しばししばまた」を例に考える。
「しばししばまた」の中には1文字のもの以外には「しばし」や「しし」という回文があるが、回文を見落とすことがないように、次の図1を用いて文字列のx文字目からy文字目までが回文かどうかをすべてのx,yの組(ただし1≦x≦y≦7)について調べる。例えば(x,y)=(1,2)は文字列「しば」に対応し、これは回文ではない。回文「しし」は(x,y)=(3,4)に対応する。また、回文「ばししば」は(x,y)=([ オ ],[ カ ])に対応する。回文に対応するマスに〇,そうでないマスに✕を記入することですべての回文が求められる。
小池さんは図1を作る際に、長い文字列に対応するマスでも〇✕を決めるために調べる文字が少なくて済む、次の方法を考えた。
まず、長さ1の文字列は回文であるため、これに対応する図1の対角線上のマス(i,i)(ただし1≦i≦7)はすべて〇となる。また、長さ2の文字列は、マス(i,i+1)(ただし1≦i≦6)に対応するが、これはそれぞれの2文字を調べることで回文かどうかを判断し、マスの〇✕を決める。
残りのマスの〇✕を決めるためには、図1において✕の左下のマスは必ず✕であるという性質を利用する。これは、
x文字目からy文字目までが回文でないとき、その両隣のx-1文字目とy+1文字目がどのような文字であっても、x-1文字目からy+1文字目までは回文にはならない
からである。一方で、
x文字目からy文字目までが回文のとき、その両隣のx-1文字目とy+1文字目が( キ )ならば、x-1文字目からy+1文字目までは回文となり、そうでないならば回文にはならない
こともわかる。
このことを使い、長さ1と2の文字列に対応するそれぞれのマスから始めて順に左下のマスの〇✕を決めていく。例えば、(x,y)=(4,4)から始めると、このマスは〇なので次は([ ク ],[ ケ ])のマスの〇✕を考える。[ ク ]文字目と[ ケ ]文字目を調べ、✕と決められる。すると、(2,[ コ ])のマス、(1,[ サ ])のマスは、それ以上文字を調べずに✕と決められる。
この方法で図1を作成するとき、文字を調べずに✕と決めるマスは全部で( シ )個である。

- 0
- 1
- 2
- 3
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問140)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問142)へ