大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問152 (情報関係基礎(第2問) 問16)
問題文
次の文章を読み、空欄( チ )に最も適当なものを、後の解答群のうちから一つ選べ。
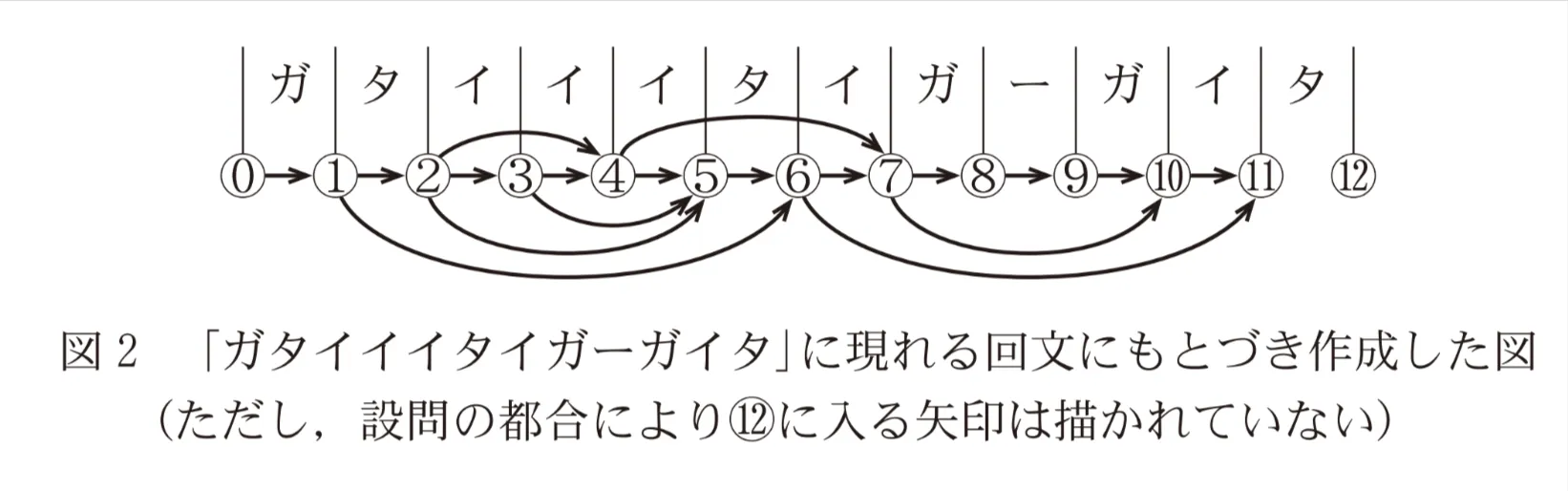
与えられた文字列を作るために連結する最も少ない回文の数(以降、最少回文数と呼ぶ。)がわかれば、その幸いさは簡単に計算できる。以下では文字列「ガタイイイタイガーガイタ」を例に、最少回文数を求める方法を考える。
小池さんは、次の図2を作成した。この図では、文字列全体の前と後および各文字の間に、図中に示す番号を振った丸印を対応させる。また、文字列中に現れるすべての回文それぞれに対して、開始直前の丸印から出て、終了直後の丸印へ入る矢印を引く。ただし、図2には設問の都合により⑫に入る矢印は描かれていない。
例えば、矢印「⓪→①」は回文「ガ」に、矢印「②→⑤」は回文「イイイ」に対応する。⑫に入る矢印は「( ス )→⑫」と「( セ )→⑫」となる。
このように表すと、例えば、「⓪→①→⑥→⑦」という3本の矢印でのたどり方は「ガ・タイイイタ・イ」の3つの回文の列に対応し、連結すると先頭から7文字目までの「ガタイイイタイ」になる。一方、連結すると同じ文字列になる「ガ・タ・イイ・イタイ」の4つの回文の列は「⓪→①→( ソ )→( タ )→⑦」という4本の矢印でのたどり方に対応する。つまり、⓪から⑦へのたどり方と、連結すると先頭から7文字目までの文字列を作る回文の列とが一対一に対応する。このことは⓪からどの丸印へのたどり方についても同様であるため、「ガタイイイタイガーガイタ」の最少回文数は⓪から⑫へたどるのに必要な矢印の最少本数(以降、最短距離と呼ぶ。)と一致する。
すべてのたどり方を考えるのは大変なので、小池さんは⓪から各丸印への最短距離を、その丸印に入る矢印に注目することで求める方法を考えた。
①に入る矢印は「⓪→①」しかない。同様に、②,③それぞれに入る矢印は「①→②」,「②→③」しかない。よって、⓪から①,②,③へのたどり方は1通りしかなく、⓪からの最短距離はそれぞれ1,( チ ),( ツ )である。
⓪から④へのたどり方は最後の矢印が「②→④」の場合と「③→④」の場合に分けられる。前者の場合は⓪から②へたどってから矢印「②→④」をたどるので、(「⓪から②への最短距離」+1)本の矢印でたどるのが最短であり、後者の場合は(「⓪から③への最短距離」+1)本の矢印でたどるのが最短である。よって、⓪から④への最短距離は( チ )+1と( ツ )+1の小さい方となる。同様に考えると、⓪から⑤へのたどり方は、最後に矢印「( テ )→⑤」をたどるのが最短であり、最短距離は( ト )となる。
以上の手順で番号の小さい順に⓪から各丸印への最短距離を求めることができ、文字列「ガタイイイタイガーガイタ」全体の最少回文数は⓪から⑫への最短距離、つまり( ナ )となる。なお、⓪から各丸印への最短距離を与える矢印のたどり方を考えると、連結して「ガタイイイタイガーガイタ」を作る( ナ )つの回文の列は( 二 )通りであることもわかる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問152(情報関係基礎(第2問) 問16) (訂正依頼・報告はこちら)
次の文章を読み、空欄( チ )に最も適当なものを、後の解答群のうちから一つ選べ。
与えられた文字列を作るために連結する最も少ない回文の数(以降、最少回文数と呼ぶ。)がわかれば、その幸いさは簡単に計算できる。以下では文字列「ガタイイイタイガーガイタ」を例に、最少回文数を求める方法を考える。
小池さんは、次の図2を作成した。この図では、文字列全体の前と後および各文字の間に、図中に示す番号を振った丸印を対応させる。また、文字列中に現れるすべての回文それぞれに対して、開始直前の丸印から出て、終了直後の丸印へ入る矢印を引く。ただし、図2には設問の都合により⑫に入る矢印は描かれていない。
例えば、矢印「⓪→①」は回文「ガ」に、矢印「②→⑤」は回文「イイイ」に対応する。⑫に入る矢印は「( ス )→⑫」と「( セ )→⑫」となる。
このように表すと、例えば、「⓪→①→⑥→⑦」という3本の矢印でのたどり方は「ガ・タイイイタ・イ」の3つの回文の列に対応し、連結すると先頭から7文字目までの「ガタイイイタイ」になる。一方、連結すると同じ文字列になる「ガ・タ・イイ・イタイ」の4つの回文の列は「⓪→①→( ソ )→( タ )→⑦」という4本の矢印でのたどり方に対応する。つまり、⓪から⑦へのたどり方と、連結すると先頭から7文字目までの文字列を作る回文の列とが一対一に対応する。このことは⓪からどの丸印へのたどり方についても同様であるため、「ガタイイイタイガーガイタ」の最少回文数は⓪から⑫へたどるのに必要な矢印の最少本数(以降、最短距離と呼ぶ。)と一致する。
すべてのたどり方を考えるのは大変なので、小池さんは⓪から各丸印への最短距離を、その丸印に入る矢印に注目することで求める方法を考えた。
①に入る矢印は「⓪→①」しかない。同様に、②,③それぞれに入る矢印は「①→②」,「②→③」しかない。よって、⓪から①,②,③へのたどり方は1通りしかなく、⓪からの最短距離はそれぞれ1,( チ ),( ツ )である。
⓪から④へのたどり方は最後の矢印が「②→④」の場合と「③→④」の場合に分けられる。前者の場合は⓪から②へたどってから矢印「②→④」をたどるので、(「⓪から②への最短距離」+1)本の矢印でたどるのが最短であり、後者の場合は(「⓪から③への最短距離」+1)本の矢印でたどるのが最短である。よって、⓪から④への最短距離は( チ )+1と( ツ )+1の小さい方となる。同様に考えると、⓪から⑤へのたどり方は、最後に矢印「( テ )→⑤」をたどるのが最短であり、最短距離は( ト )となる。
以上の手順で番号の小さい順に⓪から各丸印への最短距離を求めることができ、文字列「ガタイイイタイガーガイタ」全体の最少回文数は⓪から⑫への最短距離、つまり( ナ )となる。なお、⓪から各丸印への最短距離を与える矢印のたどり方を考えると、連結して「ガタイイイタイガーガイタ」を作る( ナ )つの回文の列は( 二 )通りであることもわかる。

- 1
- 2
- 3
- 4
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問151)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問153)へ