大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問172 (情報関係基礎(第3問) 問15)
問題文
Kさんは、あみだくじを表示するプログラムを作ろうと考えた。どの文字も同じ幅で表示されることを仮定して、記号の「┃」・「┣」・「┫」という文字と改行を使うことにした。文字の左右および行間に隙間のない表示をすれば、これらの記号がつながって、あみだくじの線に見える。
あみだくじには縦線が2本以上、横線が1本以上ある。プログラムを簡単にするため、横線は隣り合う縦線の間のみを結ぶとし、一つの行にはちょうど1本だけ横線があるとした。
例えば、縦線が3本で横線が4本であるあみだくじを、図1のように4行で表示する。この図で点線は文字の枠を示しており、各行の右端で改行している。このあみだくじの一番上の横線は左から2本目と3本目の縦線を結んでおり、「┃」・「┣」・「┫」と改行をこの順に表示することで1行目を出力できる。上から2番目の横線は左から1本目と2本目の縦線を結んでおり、1行目の表示に続けて「┣」・「┫」・「┃」と改行をこの順に表示することで2行目を出力できる。3行目と4行目も同様である。
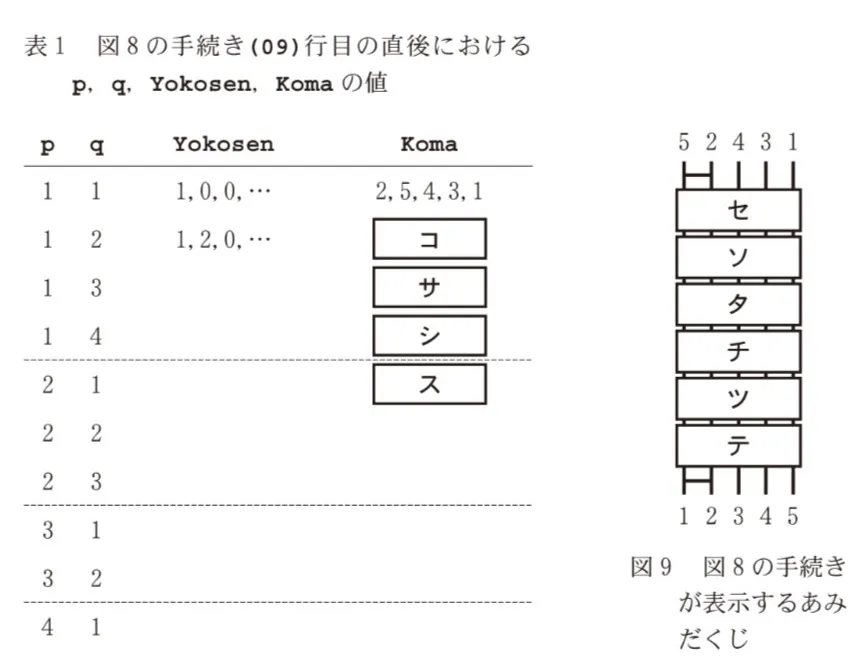
次の文章を読み、図9の空欄( ソ )に入れるのに最も適当なものを、後の解答群のうちから一つ選べ。
Kさんは次に、あみだくじを引いた結果をコンピュータで求めることを考えた。まず、あみだくじの縦線のそれぞれの上端にコマを置く。コマを区別するため、それぞれに番号をつけておく。すべてのコマを同時に、縦線に沿って下に移動していき、横線があったら、横線がつなぐ二つの縦線の上にあるコマを入れ替えれば、あみだくじの結果を求めることができる(図3)。
コマの番号を順番に格納した配列Komaが与えられ、Komaには最初、あみだくじの上端に置くコマの番号が左から順に格納されているものとする。すなわち、Komaの要素数とあみだくじの縦線の本数は等しい。
できた手続きを図5~7に示す。ここで用いている関数「要素数」はあらかじめ用意されたもので、配列を与えるとその要素数を返す。例えばKomaが[1,2,3]のとき、要素数(Koma)は3を返す。図6と図7はここで用いる新しい関数の定義である。関数を定義するときは、「関数」というキーワードと空白に続いて、関数名と、()でくくられた引数列を書き、「を」と「と定義する」までの間に関数の本体を書く。関数を呼び出すときは、関数名に続けて引数列を( )でくくって書く。例えば、図5の(01)行目は関数「配列を表示する」を呼び出しており、これを実行すると、図6の(02)~(05)行目が実行される。
図5では、まず図6で定義した関数「配列を表示する」を呼び出し、最初に与えられたKomaを表示する。次に図7で定義した関数「あみだくじを表示する」を呼び出す。ここでは[ カ ]の値がtateに格納されて、図2と同じ処理をすることであみだくじを表示する。図5の(03)~(07)行目では、コマを入れ替えることによって、あみだくじの結果を求めている。最後に(08)行目で再び関数「配列を表示する」を呼び出して結果を表示している(図4)。
図5あみだくじの結果を求める手続き
(01)配列を表示する(Koma)
(02)あみだくじを表示する([ カ ],Yokosen,要素数(Yokosen))
(03)yを1から要素数(Yokosen)まで1ずつ増やしながら、
(04)│ t←Koma[Yokosen[y]]
(05)│ ( キ )
(06)│ ( ク )
(07)を繰り返す
(08)配列を表示する(Koma)
図6関数「配列を表示する」の定義
(01)関数 配列を表示する(Koma)を
(02)│ jを1から要素数(Koma)まで1ずつ増やしながら、
(03)│ │ ( ケ )を改行なしで表示する
(04)│ を繰り返す
(05)│ 改行を表示する
(06)と定義する
図7関数「あみだくじを表示する」の定義
(01)関数 あみだくじを表示する(tate,Yokosen,yoko)を
(02−15)│ (図2と同じ)
(16)と定義する
Kさんが手続きを作るのを見ていたMさんは、昇順でないコマの並びを昇順に並べ替えるあみだくじを表示する手続きを作ることにした。配列Komaの隣り合う要素の大小関係が逆転しているときに、これらを入れ替えればよいと考えて、図8の手続きを作った。この手続きでは、図6で定義された関数「配列を表示する」と図7で定義された関数「あみだくじを表示する」を用いている。なお、配列Yokosenは十分な大きさを持ち、全要素がОで初期化されていると仮定する。
Mさんが作った図8の手続きについて、Kさんは具体的な例としてKomaに[5,2,4,3,1]を入れた場合の動作を観察した。このとき表1を用意して、図8の(09)行目の直後におけるp,q,Yokosen,Komaを記録し、その変化を見ることで実行の様子を追いかけた。最終的には図9のあみだくじが表示された。
図8昇順に並べ替えるあみだくじを作って表示する手続き
(01)配列を表示する(Koma)
(02)yoko←0
(03)pを1から要素数(Koma)-1まで1ずつ増やしながら、
(04)│ qを1から要素数(Koma)-pまで1ずつ増やしながら、
(05)│ │ もしKoma[q]>Koma[q+1]ならば
(06)│ │ │ (Koma[q]とKoma[q+1]を入れ替える手続き)
(07)│ │ │ yoko←yoko+1
(08)│ │ │ Yokosen[yoko]←q
(09)│ │ を実行する
(10)│ を繰り返す
(11)を繰り返す
(12)あみだくじを表示する([ カ ],Yokosen,yoko)
(13)配列を表示する(Koma)
図8の(04)行目の要素数(Koma)-pを要素数(Koma)-1としても同じあみだくじが表示される。しかし、( ト )の処理の結果としてp番目に大きな値の位置(添字)が決まることで、Komaの要素が大きな値順にp番目まで決まるため、要素数(Koma)-pまで繰り返せば十分である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問172(情報関係基礎(第3問) 問15) (訂正依頼・報告はこちら)
Kさんは、あみだくじを表示するプログラムを作ろうと考えた。どの文字も同じ幅で表示されることを仮定して、記号の「┃」・「┣」・「┫」という文字と改行を使うことにした。文字の左右および行間に隙間のない表示をすれば、これらの記号がつながって、あみだくじの線に見える。
あみだくじには縦線が2本以上、横線が1本以上ある。プログラムを簡単にするため、横線は隣り合う縦線の間のみを結ぶとし、一つの行にはちょうど1本だけ横線があるとした。
例えば、縦線が3本で横線が4本であるあみだくじを、図1のように4行で表示する。この図で点線は文字の枠を示しており、各行の右端で改行している。このあみだくじの一番上の横線は左から2本目と3本目の縦線を結んでおり、「┃」・「┣」・「┫」と改行をこの順に表示することで1行目を出力できる。上から2番目の横線は左から1本目と2本目の縦線を結んでおり、1行目の表示に続けて「┣」・「┫」・「┃」と改行をこの順に表示することで2行目を出力できる。3行目と4行目も同様である。
次の文章を読み、図9の空欄( ソ )に入れるのに最も適当なものを、後の解答群のうちから一つ選べ。
Kさんは次に、あみだくじを引いた結果をコンピュータで求めることを考えた。まず、あみだくじの縦線のそれぞれの上端にコマを置く。コマを区別するため、それぞれに番号をつけておく。すべてのコマを同時に、縦線に沿って下に移動していき、横線があったら、横線がつなぐ二つの縦線の上にあるコマを入れ替えれば、あみだくじの結果を求めることができる(図3)。
コマの番号を順番に格納した配列Komaが与えられ、Komaには最初、あみだくじの上端に置くコマの番号が左から順に格納されているものとする。すなわち、Komaの要素数とあみだくじの縦線の本数は等しい。
できた手続きを図5~7に示す。ここで用いている関数「要素数」はあらかじめ用意されたもので、配列を与えるとその要素数を返す。例えばKomaが[1,2,3]のとき、要素数(Koma)は3を返す。図6と図7はここで用いる新しい関数の定義である。関数を定義するときは、「関数」というキーワードと空白に続いて、関数名と、()でくくられた引数列を書き、「を」と「と定義する」までの間に関数の本体を書く。関数を呼び出すときは、関数名に続けて引数列を( )でくくって書く。例えば、図5の(01)行目は関数「配列を表示する」を呼び出しており、これを実行すると、図6の(02)~(05)行目が実行される。
図5では、まず図6で定義した関数「配列を表示する」を呼び出し、最初に与えられたKomaを表示する。次に図7で定義した関数「あみだくじを表示する」を呼び出す。ここでは[ カ ]の値がtateに格納されて、図2と同じ処理をすることであみだくじを表示する。図5の(03)~(07)行目では、コマを入れ替えることによって、あみだくじの結果を求めている。最後に(08)行目で再び関数「配列を表示する」を呼び出して結果を表示している(図4)。
図5あみだくじの結果を求める手続き
(01)配列を表示する(Koma)
(02)あみだくじを表示する([ カ ],Yokosen,要素数(Yokosen))
(03)yを1から要素数(Yokosen)まで1ずつ増やしながら、
(04)│ t←Koma[Yokosen[y]]
(05)│ ( キ )
(06)│ ( ク )
(07)を繰り返す
(08)配列を表示する(Koma)
図6関数「配列を表示する」の定義
(01)関数 配列を表示する(Koma)を
(02)│ jを1から要素数(Koma)まで1ずつ増やしながら、
(03)│ │ ( ケ )を改行なしで表示する
(04)│ を繰り返す
(05)│ 改行を表示する
(06)と定義する
図7関数「あみだくじを表示する」の定義
(01)関数 あみだくじを表示する(tate,Yokosen,yoko)を
(02−15)│ (図2と同じ)
(16)と定義する
Kさんが手続きを作るのを見ていたMさんは、昇順でないコマの並びを昇順に並べ替えるあみだくじを表示する手続きを作ることにした。配列Komaの隣り合う要素の大小関係が逆転しているときに、これらを入れ替えればよいと考えて、図8の手続きを作った。この手続きでは、図6で定義された関数「配列を表示する」と図7で定義された関数「あみだくじを表示する」を用いている。なお、配列Yokosenは十分な大きさを持ち、全要素がОで初期化されていると仮定する。
Mさんが作った図8の手続きについて、Kさんは具体的な例としてKomaに[5,2,4,3,1]を入れた場合の動作を観察した。このとき表1を用意して、図8の(09)行目の直後におけるp,q,Yokosen,Komaを記録し、その変化を見ることで実行の様子を追いかけた。最終的には図9のあみだくじが表示された。
図8昇順に並べ替えるあみだくじを作って表示する手続き
(01)配列を表示する(Koma)
(02)yoko←0
(03)pを1から要素数(Koma)-1まで1ずつ増やしながら、
(04)│ qを1から要素数(Koma)-pまで1ずつ増やしながら、
(05)│ │ もしKoma[q]>Koma[q+1]ならば
(06)│ │ │ (Koma[q]とKoma[q+1]を入れ替える手続き)
(07)│ │ │ yoko←yoko+1
(08)│ │ │ Yokosen[yoko]←q
(09)│ │ を実行する
(10)│ を繰り返す
(11)を繰り返す
(12)あみだくじを表示する([ カ ],Yokosen,yoko)
(13)配列を表示する(Koma)
図8の(04)行目の要素数(Koma)-pを要素数(Koma)-1としても同じあみだくじが表示される。しかし、( ト )の処理の結果としてp番目に大きな値の位置(添字)が決まることで、Komaの要素が大きな値順にp番目まで決まるため、要素数(Koma)-pまで繰り返せば十分である。

- ┃┃┃┃┃
- ┣┫┃┃┃
- ┃┣┫┃┃
- ┃┃┣┫┃
- ┃┃┃┣┫
- ┣┫┃┣┫
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問171)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問173)へ