大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問13 (数学Ⅰ・数学A(第2問) 問1)
問題文
高校1年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は1皿あたりの価格をいくらにするかを検討するためにアンケート調査を行い、1皿あたりの価格と売り上げ数の関係について次のように予測した。
1皿あたりの価格:100円 売り上げ数:1250皿
1皿あたりの価格:150円 売り上げ数:750皿
1皿あたりの価格:200円 売り上げ数:450皿
1皿あたりの価格:250円 売り上げ数:250皿
1皿あたりの価格:300円 売り上げ数:50皿
この結果から太郎さんと花子さんは、1皿あたりの価格が100円以上300円以下の範囲で、予測される利益(以下、利益)の最大値について考えることにした。
太郎:価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
花子:散布図の点の並びは、1次関数のグラフのようには見えないね。2次関数のグラフみたいに見えるよ。
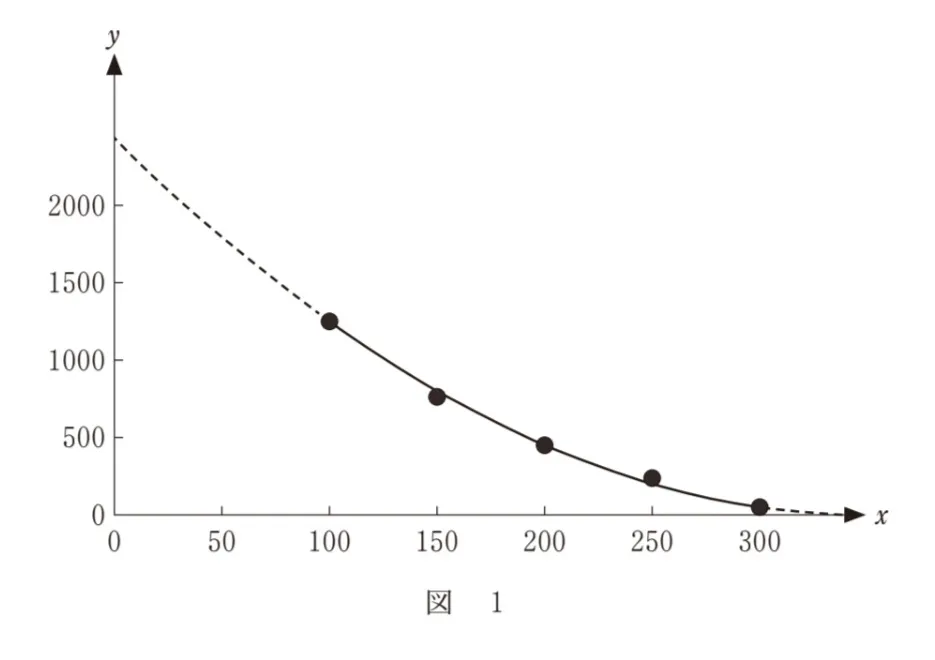
太郎:価格が100、200、300のときの点を通る2次関数のグラフをかくと、図1のように価格が150、250のときの点もそのグラフの近くにあるよ。
花子:現実には、もっと複雑な関係なのだろうけど、1次関数と2次関数で比べると、2次関数で考えた方がよいような気がするね。
2次関数
y=ax2+bx+c ・・・・・①
のグラフは、3点(100,1250)、(200,450)、(300,50)を通るとする。このとき、b=( アイウ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問13(数学Ⅰ・数学A(第2問) 問1) (訂正依頼・報告はこちら)
高校1年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は1皿あたりの価格をいくらにするかを検討するためにアンケート調査を行い、1皿あたりの価格と売り上げ数の関係について次のように予測した。
1皿あたりの価格:100円 売り上げ数:1250皿
1皿あたりの価格:150円 売り上げ数:750皿
1皿あたりの価格:200円 売り上げ数:450皿
1皿あたりの価格:250円 売り上げ数:250皿
1皿あたりの価格:300円 売り上げ数:50皿
この結果から太郎さんと花子さんは、1皿あたりの価格が100円以上300円以下の範囲で、予測される利益(以下、利益)の最大値について考えることにした。
太郎:価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
花子:散布図の点の並びは、1次関数のグラフのようには見えないね。2次関数のグラフみたいに見えるよ。
太郎:価格が100、200、300のときの点を通る2次関数のグラフをかくと、図1のように価格が150、250のときの点もそのグラフの近くにあるよ。
花子:現実には、もっと複雑な関係なのだろうけど、1次関数と2次関数で比べると、2次関数で考えた方がよいような気がするね。
2次関数
y=ax2+bx+c ・・・・・①
のグラフは、3点(100,1250)、(200,450)、(300,50)を通るとする。このとき、b=( アイウ )である。

- −13
- −14
- −15
- −16
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
正解は -14 です。
解く際の順序は
①式に代入する
②未知の値を1つにする
③連立方程式を作る
です。
①式に代入する
まず、y=ax2+bx+cに
3点(100,1250)、(200,450)、(300,50)を
代入します。
すると、以下の式が作られます。
(100,1250)を代入した式
1250=10000a+100b+c …式A
(200,450)を代入した式
450=40000a+200b+c …式B
(300,50)を代入した式
50=90000a+300b+c …式C
②未知の値を1つにする
未知の値a,b,cのうち1つを消して
連立方程式を立てたいため、
cを消します。
A-B
800=-30000a-100b
両辺を100で割って
8=-300a-b …式D
B-C
400=-50000a-100b
両辺を100で割って
4=-500a-b …式E
無事cが消えました。
式Dと式Eで連立方程式を作ります。
③連立方程式を作る
40=-1500a-5b …式D×5
―) 12=-1500a-3b …式E×3
28=-2b
両辺を2で割って
14=-b
よって答えはb=-14となります。
不正解です。
正解です。
不正解です。
不正解です。
とりあえず、式と(x,y)が提示されたら、
代入してみることをお勧めします。
参考になった数0
この解説の修正を提案する
前の問題(問12)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問14)へ