大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問18 (数学Ⅰ・数学A(第2問) 問6)
問題文
高校1年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は1皿あたりの価格をいくらにするかを検討するためにアンケート調査を行い、1皿あたりの価格と売り上げ数の関係について次のように予測した。
1皿あたりの価格:100円 売り上げ数:1250皿
1皿あたりの価格:150円 売り上げ数:750皿
1皿あたりの価格:200円 売り上げ数:450皿
1皿あたりの価格:250円 売り上げ数:250皿
1皿あたりの価格:300円 売り上げ数:50皿
この結果から太郎さんと花子さんは、1皿あたりの価格が100円以上300円以下の範囲で、予測される利益(以下、利益)の最大値について考えることにした。
太郎:価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
花子:散布図の点の並びは、1次関数のグラフのようには見えないね。2次関数のグラフみたいに見えるよ。
太郎:価格が100、200、300のときの点を通る2次関数のグラフをかくと、図1のように価格が150、250のときの点もそのグラフの近くにあるよ。
花子:現実には、もっと複雑な関係なのだろうけど、1次関数と2次関数で比べると、2次関数で考えた方がよいような気がするね。
2次関数
y=ax2+bx+c ・・・・・①
のグラフは、3点(100,1250)、(200,450)、(300,50)を通るとする。このとき、b=( アイウ )である。
二人は、1皿あたりの価格xと売り上げ数yの関係が①を満たしたときの、100≦x≦300での利益の最大値Mについて考えることにした。
1皿あたりの材料費は80円であり、材料費以外にかかる費用は5000円である。よって、x−80と売り上げ数の積から、5000を引いたものが利益となる。
このとき、売り上げ数を①の右辺の2次式とすると、利益はxの( エ )次式となる。一方で、売り上げ数として①の右辺の代わりにxの( オ )次式を使えば、利益はxの2次式となる。
太郎:利益が( エ )次式だと、今の私たちの知識では最大値Mを正確に求めることができないね。
花子:①の右辺の代わりに( オ )次式を使えば利益は2次式になるから、最大値を求められるよ。
太郎:現実の問題を考えるときには正確な答えが出せないことも多いから、自分の知識の範囲内で工夫しておおよその値を出すことには価値があると思うよ。
花子:考えているのが利益だから、①の右辺の代わりの式は売り上げ数を少なく見積もった式を考えると手堅いね。
太郎:少なく見積もるということは、その関数のグラフは①のグラフより、下の方にあるということだね。
1次関数
y=−4x+1160 ・・・・・②
を考える。このとき、①と②のグラフの位置関係は後の図2のようになっている。
①の右辺の代わりに②の右辺を使うと、売り上げ数を少なく見積もることになる。売り上げ数を②の右辺としたときの利益zは
z=−( カ )x2+( キクケコ )x−97800
で与えられる。zが最大となるxをpとおくと、p=( サシス )であり、zの最大値は39100である。
太郎:売り上げ数を少なく見積もった式は、各xについて値が①より小さければよいので、色々な式が考えられるね。
花子:それらの式を①の右辺の代わりに使ったときの利益の最大値と、①の右辺から計算される利益の最大値Mとの関係はどうなるのかな。
1次関数
y=−8x+1968 ・・・・・③
を考える。売り上げ数を③の右辺としたときの利益はx=163のときに最大となり、最大値は50112となる。
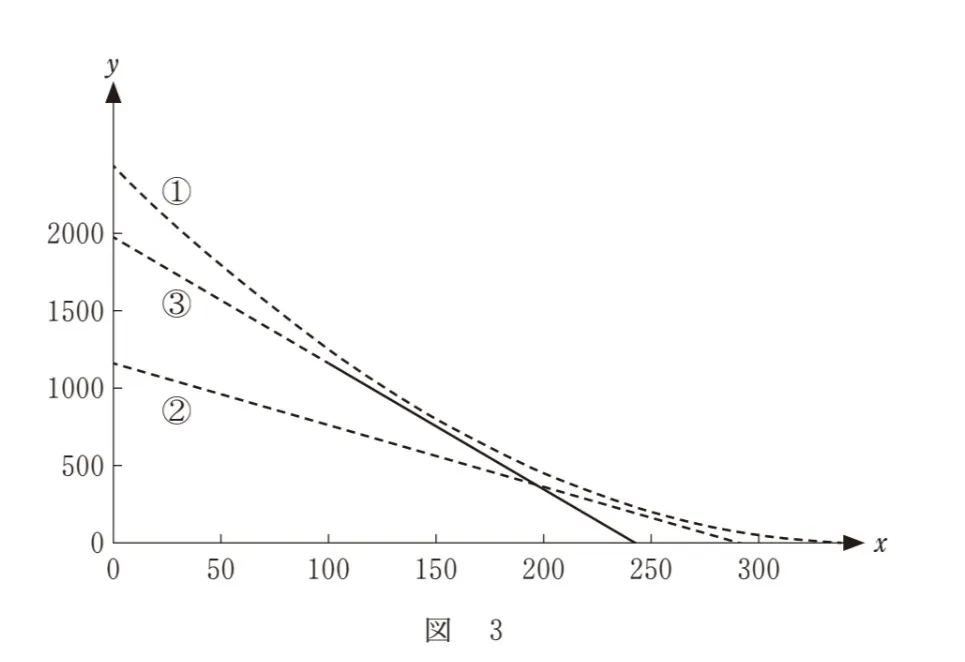
また、①~③のグラフの位置関係は後の図3のようになっている。
売り上げ数を①の右辺としたときの利益の記述として、正しいものは( セ )と( ソ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問18(数学Ⅰ・数学A(第2問) 問6) (訂正依頼・報告はこちら)
高校1年生の太郎さんと花子さんのクラスでは、文化祭でやきそば屋を出店することになった。二人は1皿あたりの価格をいくらにするかを検討するためにアンケート調査を行い、1皿あたりの価格と売り上げ数の関係について次のように予測した。
1皿あたりの価格:100円 売り上げ数:1250皿
1皿あたりの価格:150円 売り上げ数:750皿
1皿あたりの価格:200円 売り上げ数:450皿
1皿あたりの価格:250円 売り上げ数:250皿
1皿あたりの価格:300円 売り上げ数:50皿
この結果から太郎さんと花子さんは、1皿あたりの価格が100円以上300円以下の範囲で、予測される利益(以下、利益)の最大値について考えることにした。
太郎:価格を横軸、売り上げ数を縦軸にとって散布図をかいてみたよ。
花子:散布図の点の並びは、1次関数のグラフのようには見えないね。2次関数のグラフみたいに見えるよ。
太郎:価格が100、200、300のときの点を通る2次関数のグラフをかくと、図1のように価格が150、250のときの点もそのグラフの近くにあるよ。
花子:現実には、もっと複雑な関係なのだろうけど、1次関数と2次関数で比べると、2次関数で考えた方がよいような気がするね。
2次関数
y=ax2+bx+c ・・・・・①
のグラフは、3点(100,1250)、(200,450)、(300,50)を通るとする。このとき、b=( アイウ )である。
二人は、1皿あたりの価格xと売り上げ数yの関係が①を満たしたときの、100≦x≦300での利益の最大値Mについて考えることにした。
1皿あたりの材料費は80円であり、材料費以外にかかる費用は5000円である。よって、x−80と売り上げ数の積から、5000を引いたものが利益となる。
このとき、売り上げ数を①の右辺の2次式とすると、利益はxの( エ )次式となる。一方で、売り上げ数として①の右辺の代わりにxの( オ )次式を使えば、利益はxの2次式となる。
太郎:利益が( エ )次式だと、今の私たちの知識では最大値Mを正確に求めることができないね。
花子:①の右辺の代わりに( オ )次式を使えば利益は2次式になるから、最大値を求められるよ。
太郎:現実の問題を考えるときには正確な答えが出せないことも多いから、自分の知識の範囲内で工夫しておおよその値を出すことには価値があると思うよ。
花子:考えているのが利益だから、①の右辺の代わりの式は売り上げ数を少なく見積もった式を考えると手堅いね。
太郎:少なく見積もるということは、その関数のグラフは①のグラフより、下の方にあるということだね。
1次関数
y=−4x+1160 ・・・・・②
を考える。このとき、①と②のグラフの位置関係は後の図2のようになっている。
①の右辺の代わりに②の右辺を使うと、売り上げ数を少なく見積もることになる。売り上げ数を②の右辺としたときの利益zは
z=−( カ )x2+( キクケコ )x−97800
で与えられる。zが最大となるxをpとおくと、p=( サシス )であり、zの最大値は39100である。
太郎:売り上げ数を少なく見積もった式は、各xについて値が①より小さければよいので、色々な式が考えられるね。
花子:それらの式を①の右辺の代わりに使ったときの利益の最大値と、①の右辺から計算される利益の最大値Mとの関係はどうなるのかな。
1次関数
y=−8x+1968 ・・・・・③
を考える。売り上げ数を③の右辺としたときの利益はx=163のときに最大となり、最大値は50112となる。
また、①~③のグラフの位置関係は後の図3のようになっている。
売り上げ数を①の右辺としたときの利益の記述として、正しいものは( セ )と( ソ )である。

- 利益の最大値Mは39100である。
- 利益の最大値Mは50112である。
- 利益の最大値Mは(39100+50112)/2である。
- x=163とすれば、利益は少なくとも50112以上となる。
- x=pとすれば、利益は少なくとも39100以上となる。
- x=163のときに利益は最大値Mをとる。
- x=pのときに利益は最大値Mをとる。
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
読解問題です。
一旦計算の手を止め、今まで算出した情報とにらめっこしましょう。
全く難しいことは言ってないので、
考えすぎずにシンプルに向き合ってみます。
今まで出てきた情報を整理すると・・・
‣2次関数
y=ax2+bx+c ・・・・・①
(1皿あたりの価格と売り上げ数のグラフ)
‣①より少なく少なく見積もった1次関数(1)
y=−4x+1160 ・・・・・②
①の右辺の代わりに②の右辺を使ったときの利益zの式
z=−4x2+1480x−97800
zの最大値 39100
zが最大となるxをpとおくと、p=185
‣①より少なく少なく見積もった1次関数(2)
y=−8x+1968 ・・・・・③
①の右辺の代わりに③の右辺を使ったときの利益zの式
z=(x-80)(-8x+1968)-5000
zの最大値 50112 (x=168のとき)
‣グラフの位置関係
①の下に②③が位置している。
これらの情報を基に、
①の式の記述として正しい選択肢を選んでみましょう。
不正解です。
利益の最大値が39100になるのは②の式です。
②は①より少なく少なく見積もった式であるため、
①の利益の最大値は39100より大きいと予想できます。
不正解です。
利益の最大値が50112になるのは③の式です。
③は①より少なく少なく見積もった式であるため、
①の利益の最大値は50112より大きいと予想できます。
不正解です。
平均取ればいいってものじゃありません。
③の式は利益の最大値が50112であるかつ、
①より少なく少なく見積もった式であるため、
①の利益の最大値は50112より大きいと予想できます。
正解です◎
③の式では、x=168のとき利益は最大値であり50112になります。
③は①より少なく少なく見積もった式であるため、
①の利益の最大値は50112より大きいと予想できます。
正解です◎
②の式では、zが最大となるxをpとおいており、
利益の最大値は39100です。
②は①より少なく少なく見積もった式であるため、
①の利益の最大値は39100より大きいと予想できます。
不正解です。
x=163のときに利益が最大になるのは③の式です。
x=163のときに①の利益の最大値をとるとは言えません。
不正解です。
②の式では、zが最大となるxをpとおいているのは②の式の場合です。
p=185のときに利益が最大になるのは②の式です。
x=p=185のときに①の利益の最大値をとるとは言えません。
情報を整理するとなんてことない問題です。
もし頭がこんがらがって分からないときは一回飛ばして違う問題に行きましょう。
それかありえない選択肢を排除して消去法で考えましょう。
参考になった数0
この解説の修正を提案する
前の問題(問17)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問19)へ