大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問72 (数学Ⅱ・数学B(第2問) 問5)
問題文
縦の長さが9cm、横の長さが24cmの長方形の厚紙がある。この厚紙から容積が最大となる箱を作る。このとき、箱にふたがない場合とふたがある場合で容積の最大値がどう変わるかを調べたい。ただし、厚紙の厚さは考えず、作る箱の形を直方体とみなす。
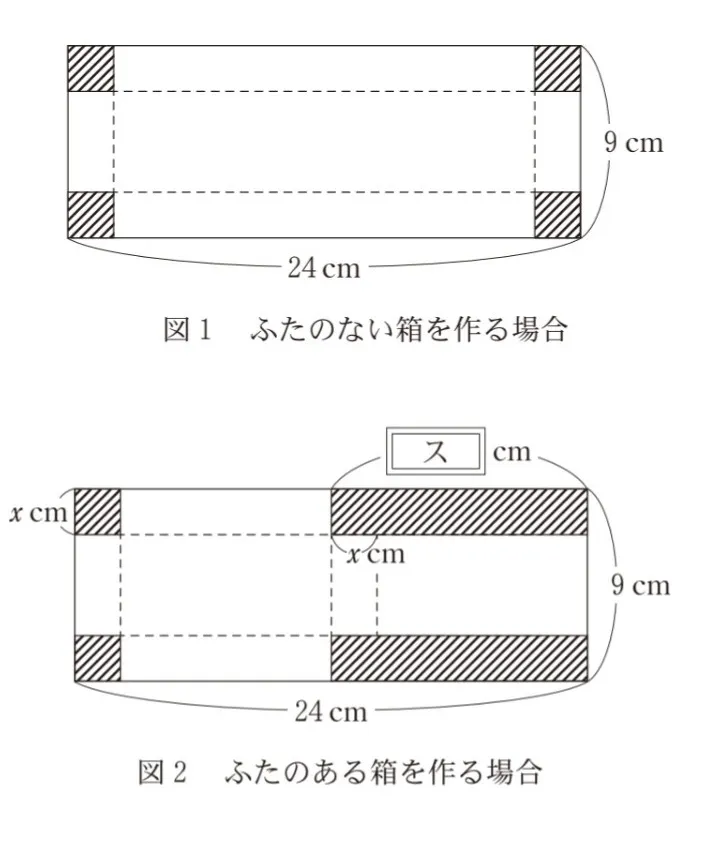
(1)厚紙の四隅(すみ)から図1のように四つの合同な正方形の斜線部分を切り取り、破線にそって折り曲げて、ふたのない箱を作る。この箱の容積をVcm3とする。
次の構想に基づいて箱の容積の最大値を考える。
<構想>
図1のように切り取る斜線部分の正方形の一辺の長さをxcmとする。Vをxの関数として表し、箱が作れるxの値の範囲に注意してVの最大値を考える。
箱が作れるためのxのとり得る値の範囲は0<x<( ア )/( イ )である。Vをxの式で表すと
V=( ウ )x3−( エオ )x2+( カキク )x
であり、Vはx=( ケ )で最大値( コサシ )をとる。
(2)厚紙の四隅から図2のように四つの斜線部分を切り取り、破線にそって折り曲げて、ふたでぴったりと閉じることのできる箱を作る。この箱の容積をWcm3とする。
図2の四つの斜線部分のうち、左側二つの斜線部分をそれぞれ一辺の長さがxcmの正方形とすると、右側二つの斜線部分は、それぞれ縦の長さがxcm、横の長さが( ス )cmの長方形となる。
太郎さんと花子さんは、Wをxの式で表した後、(1)の結果を見ながらWの最大値の求め方について話している。
太郎:Wの式がわかったから、Wの最大値は、(1)と同じように求められるね。
花子:ちょっと待って。Wを表す式と、(1)のVを表す式は似ているね。Wを表す式とVを表す式の関係を利用できないかな。
(1)のVが最大値をとるときのxの値をx0とする。Wの最大値は(1)で求めたVの最大値( セ )。また、Wが最大値をとるxは( ソ )。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問72(数学Ⅱ・数学B(第2問) 問5) (訂正依頼・報告はこちら)
縦の長さが9cm、横の長さが24cmの長方形の厚紙がある。この厚紙から容積が最大となる箱を作る。このとき、箱にふたがない場合とふたがある場合で容積の最大値がどう変わるかを調べたい。ただし、厚紙の厚さは考えず、作る箱の形を直方体とみなす。
(1)厚紙の四隅(すみ)から図1のように四つの合同な正方形の斜線部分を切り取り、破線にそって折り曲げて、ふたのない箱を作る。この箱の容積をVcm3とする。
次の構想に基づいて箱の容積の最大値を考える。
<構想>
図1のように切り取る斜線部分の正方形の一辺の長さをxcmとする。Vをxの関数として表し、箱が作れるxの値の範囲に注意してVの最大値を考える。
箱が作れるためのxのとり得る値の範囲は0<x<( ア )/( イ )である。Vをxの式で表すと
V=( ウ )x3−( エオ )x2+( カキク )x
であり、Vはx=( ケ )で最大値( コサシ )をとる。
(2)厚紙の四隅から図2のように四つの斜線部分を切り取り、破線にそって折り曲げて、ふたでぴったりと閉じることのできる箱を作る。この箱の容積をWcm3とする。
図2の四つの斜線部分のうち、左側二つの斜線部分をそれぞれ一辺の長さがxcmの正方形とすると、右側二つの斜線部分は、それぞれ縦の長さがxcm、横の長さが( ス )cmの長方形となる。
太郎さんと花子さんは、Wをxの式で表した後、(1)の結果を見ながらWの最大値の求め方について話している。
太郎:Wの式がわかったから、Wの最大値は、(1)と同じように求められるね。
花子:ちょっと待って。Wを表す式と、(1)のVを表す式は似ているね。Wを表す式とVを表す式の関係を利用できないかな。
(1)のVが最大値をとるときのxの値をx0とする。Wの最大値は(1)で求めたVの最大値( セ )。また、Wが最大値をとるxは( ソ )。

- の1/4倍である
- の4倍である
- の1/3倍である
- の3倍である
- の1/2倍である
- の2倍である
- と等しくなる
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問71)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問73)へ