大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問150 (情報関係基礎(第2問) 問14)
問題文
AさんにはSNS上で遊ぶお気に入りのゲームがある。このゲーム内では相互に友達の申請をすると「友達」になれる。友達になることでメッセージのやり取りが可能となり、情報を共有することができる。複数人で協力することでゲームを有利に進められるため、Aさんは協力プレイを呼びかけるメッセージを送ってからゲームを始めるようにしている。なお、メッセージは1回で友達全員に届く。Aさんと同じクラスの生徒のうち、Aさんを含めて9名がこのゲームをプレイしている。
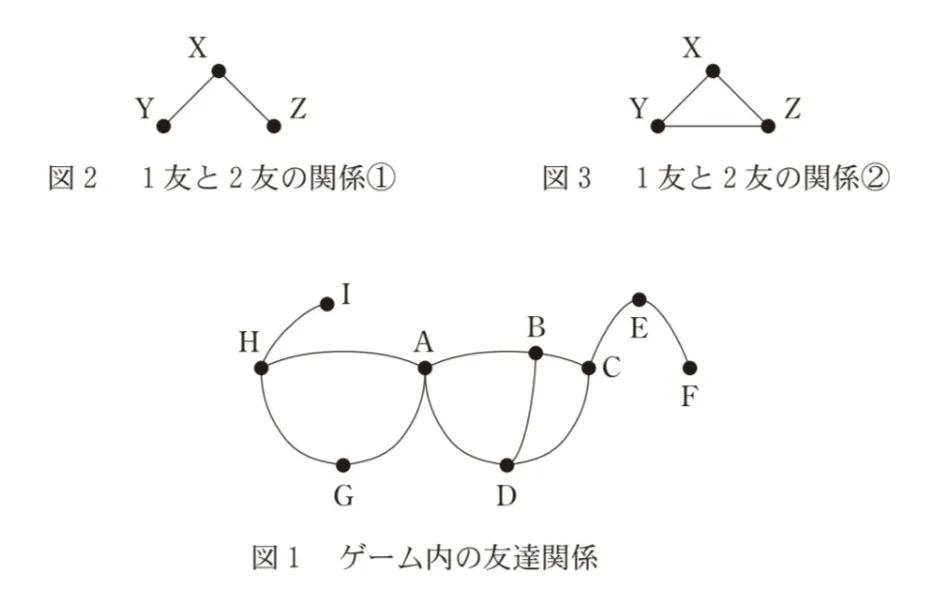
ゲーム内の9名の友達関係を次の図1に示す。図1において点Aから点Iは生徒を表しており、友達である生徒同士は線で結ばれている。
Aさんは友達の友達にもメッセージを共有してもらえれば、さらにゲームが有利に進められると考えた。そこで、友達関係を拡張して「友達の友達もみんな友達」という視点で考えることにした。
あるXさんを基準としたとき、Xさんの友達を1友、Xさんの友達の友達を2友と考える。つまり、Xさんから線をe本たどった先の人をe友(eは1以上の整数)とする。
たまたまAさんに予定がありゲームをプレイできない日があった。後日Aさんは友達から、その日は協力プレイの人数が集まらずゲームが進まなかったと言われた。そこでAさんは、ゲームを休む人がいることと、情報が共有できなくなることとの関係を考えることにした。
まず初めに次の図2の状況を考える。このときXは、自分自身が2友であることをふまえると( ス )であり、Xがゲームを休むと残りの全員は同じ情報を共有できない。しかし、YやZも同様に( ス )であるが、ゲームを休んでも残りの全員は同じ情報を共有できる。次に、図3の状況を考えてみた。このとき、Xは( セ )であり、Xがゲームを休んでも残りの全員は同じ情報を共有できる。そのため、Aさんは1友と2友の関係において( セ )を考えることで、そのひと一人が休んでも、残りの全員は同じ情報を共有できると考えた。Aさんは、図3のような関係を三角形と呼ぶことにした。
そこでAさんは、図1において三角形のメンバーになっている人を調べてみたところ、Aさん、Bさん、Cさん、Dさん、Gさん、Hさんの6名であった。この中で、( セ )は例えばDさんが該当する。ほかに( セ )に該当するのは( ソ )、( タ )、( チ )で合わせて4名である。Aさんは、この4名はゲームを休んでも残りの全員が同じ情報を共有できると考えたが、図1を見るとこの4名のうち( ツ )がゲームを休むと全員が同じ情報を共有できなくなる。そのためAさんは、全員が情報共有できるためのより正確な条件を考えてみた。図1において、あるXさんが( セ )であるとき、次の(1)か(2)のどちらかを満たせば、Xさんが休んでも残りの全員は情報共有できることにAさんは気付いた。
(1)Xさんが一つだけの三角形のメンバーであれば、休んでも残りの全員は情報共有できる。このXさんとして( テ )が該当する。
(2)Xさんが二つ以上の三角形のメンバーであり、これらの三角形のうち、任意の三角形がそれ以外の少なくとも一つの三角形と同じ線を共有するのであれば、休んでも残りの全員は情報共有できる。このXさんとしてDさんと( ト )が該当する。
また、1友の数が一人である生徒はゲームを休んでも残りの全員は情報共有でき、二人いることがわかった。
Aさんはこれらの結果から、休むと全員が情報共有できなくなる可能性のある人には早めに声をかけることとし、「明日来てくれるかな?」とお昼休みに呼びかけることにした。
( ツ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問150(情報関係基礎(第2問) 問14) (訂正依頼・報告はこちら)
AさんにはSNS上で遊ぶお気に入りのゲームがある。このゲーム内では相互に友達の申請をすると「友達」になれる。友達になることでメッセージのやり取りが可能となり、情報を共有することができる。複数人で協力することでゲームを有利に進められるため、Aさんは協力プレイを呼びかけるメッセージを送ってからゲームを始めるようにしている。なお、メッセージは1回で友達全員に届く。Aさんと同じクラスの生徒のうち、Aさんを含めて9名がこのゲームをプレイしている。
ゲーム内の9名の友達関係を次の図1に示す。図1において点Aから点Iは生徒を表しており、友達である生徒同士は線で結ばれている。
Aさんは友達の友達にもメッセージを共有してもらえれば、さらにゲームが有利に進められると考えた。そこで、友達関係を拡張して「友達の友達もみんな友達」という視点で考えることにした。
あるXさんを基準としたとき、Xさんの友達を1友、Xさんの友達の友達を2友と考える。つまり、Xさんから線をe本たどった先の人をe友(eは1以上の整数)とする。
たまたまAさんに予定がありゲームをプレイできない日があった。後日Aさんは友達から、その日は協力プレイの人数が集まらずゲームが進まなかったと言われた。そこでAさんは、ゲームを休む人がいることと、情報が共有できなくなることとの関係を考えることにした。
まず初めに次の図2の状況を考える。このときXは、自分自身が2友であることをふまえると( ス )であり、Xがゲームを休むと残りの全員は同じ情報を共有できない。しかし、YやZも同様に( ス )であるが、ゲームを休んでも残りの全員は同じ情報を共有できる。次に、図3の状況を考えてみた。このとき、Xは( セ )であり、Xがゲームを休んでも残りの全員は同じ情報を共有できる。そのため、Aさんは1友と2友の関係において( セ )を考えることで、そのひと一人が休んでも、残りの全員は同じ情報を共有できると考えた。Aさんは、図3のような関係を三角形と呼ぶことにした。
そこでAさんは、図1において三角形のメンバーになっている人を調べてみたところ、Aさん、Bさん、Cさん、Dさん、Gさん、Hさんの6名であった。この中で、( セ )は例えばDさんが該当する。ほかに( セ )に該当するのは( ソ )、( タ )、( チ )で合わせて4名である。Aさんは、この4名はゲームを休んでも残りの全員が同じ情報を共有できると考えたが、図1を見るとこの4名のうち( ツ )がゲームを休むと全員が同じ情報を共有できなくなる。そのためAさんは、全員が情報共有できるためのより正確な条件を考えてみた。図1において、あるXさんが( セ )であるとき、次の(1)か(2)のどちらかを満たせば、Xさんが休んでも残りの全員は情報共有できることにAさんは気付いた。
(1)Xさんが一つだけの三角形のメンバーであれば、休んでも残りの全員は情報共有できる。このXさんとして( テ )が該当する。
(2)Xさんが二つ以上の三角形のメンバーであり、これらの三角形のうち、任意の三角形がそれ以外の少なくとも一つの三角形と同じ線を共有するのであれば、休んでも残りの全員は情報共有できる。このXさんとしてDさんと( ト )が該当する。
また、1友の数が一人である生徒はゲームを休んでも残りの全員は情報共有でき、二人いることがわかった。
Aさんはこれらの結果から、休むと全員が情報共有できなくなる可能性のある人には早めに声をかけることとし、「明日来てくれるかな?」とお昼休みに呼びかけることにした。
( ツ )にあてはまるものを1つ選べ。

- Aさん
- Bさん
- Cさん
- Dさん
- Eさん
- Fさん
- Gさん
- Hさん
- Iさん
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問149)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問151)へ