大学入学共通テスト(数学) 過去問
令和4年度(2022年度)本試験
問27 (数学Ⅰ・数学A(第2問) 問15)
問題文
〔2〕日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では「海外日本語教育機関調査」を実施しており、各国における教育機関数、教員数、学習者数が調べられている。2018年度において学習者数が5000人以上の国と地域(以下、国)は29か国であった。これら29か国について、2009年度と2018年度のデータが得られている。
(3)各国における2018年度の学習者数を100としたときの2009年度の学習者数S,および、各国における2018年度の教員数を100としたときの2009年度の教員数Tを算出した。
例えば、学習者数について説明すると、ある国において、2009年度が44272人、2018年度が174521人であった場合、2009年度の学習者数Sは44272/174521✕100より25.4と算出される。
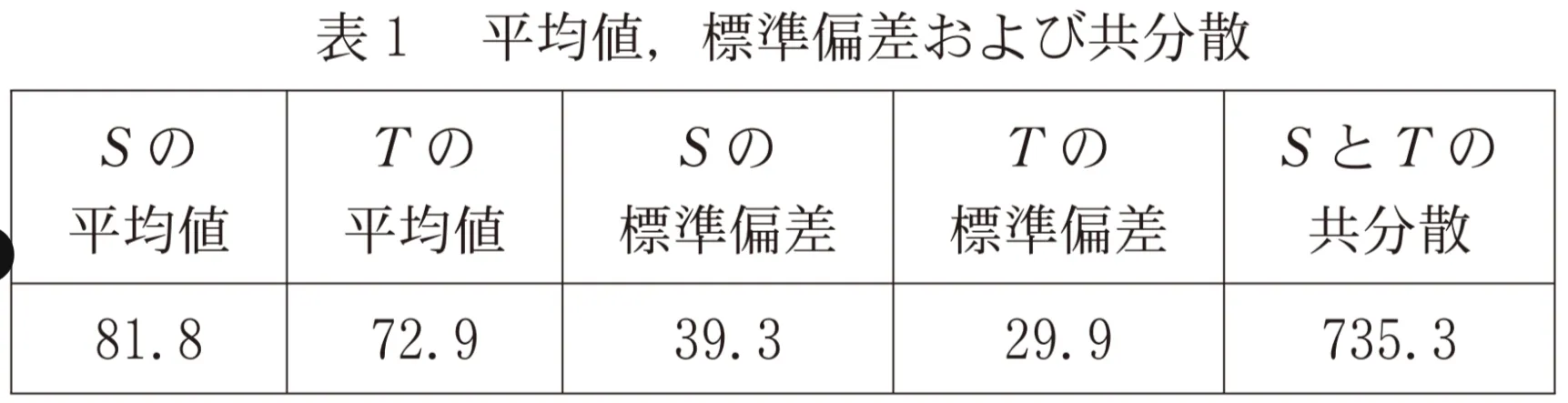
表1はSとTについて、平均値、標準偏差および共分散を計算したものである。ただし、SとTの共分散は、Sの偏差とTの偏差の積の平均値である。
表1の数値が四捨五入していない正確な値であるとして、SとTの相関係数を求めると( ソ ).( タチ )である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和4年度(2022年度)本試験 問27(数学Ⅰ・数学A(第2問) 問15) (訂正依頼・報告はこちら)
〔2〕日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では「海外日本語教育機関調査」を実施しており、各国における教育機関数、教員数、学習者数が調べられている。2018年度において学習者数が5000人以上の国と地域(以下、国)は29か国であった。これら29か国について、2009年度と2018年度のデータが得られている。
(3)各国における2018年度の学習者数を100としたときの2009年度の学習者数S,および、各国における2018年度の教員数を100としたときの2009年度の教員数Tを算出した。
例えば、学習者数について説明すると、ある国において、2009年度が44272人、2018年度が174521人であった場合、2009年度の学習者数Sは44272/174521✕100より25.4と算出される。
表1はSとTについて、平均値、標準偏差および共分散を計算したものである。ただし、SとTの共分散は、Sの偏差とTの偏差の積の平均値である。
表1の数値が四捨五入していない正確な値であるとして、SとTの相関係数を求めると( ソ ).( タチ )である。

- 0.35
- 0.61
- 0.63
- 1.61
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問26)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問28)へ