大学入学共通テスト（数学） 過去問
令和4年度（2022年度）本試験
問111 (数学Ⅱ・数学B（第5問） 問7)
問題文
空欄（ コ／サt−シ ）に当てはまるものを選べ。 
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
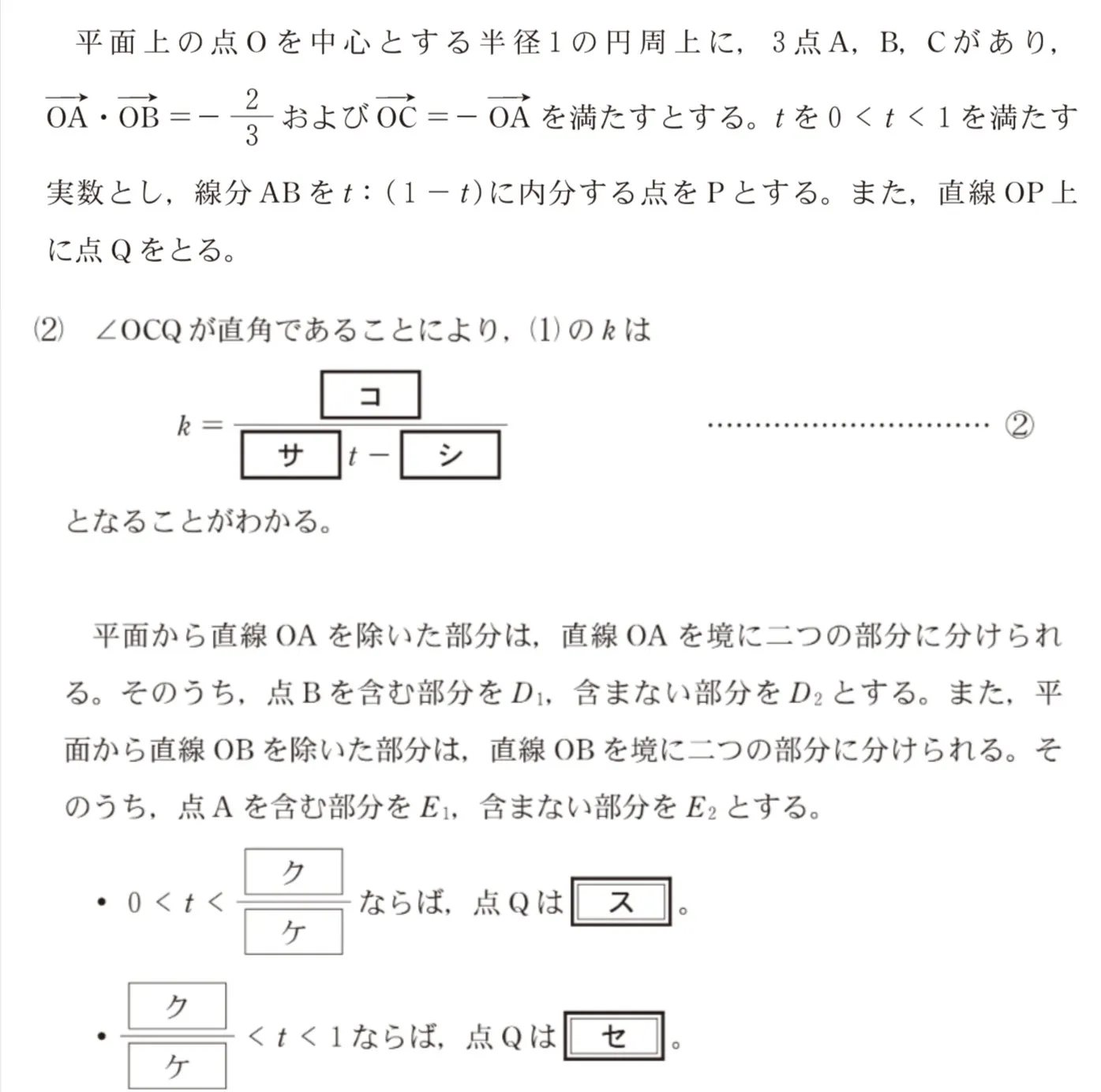
大学入学共通テスト（数学）試験 令和4年度（2022年度）本試験 問111（数学Ⅱ・数学B（第5問） 問7） （訂正依頼・報告はこちら）
空欄（ コ／サt−シ ）に当てはまるものを選べ。
- コ：3 サ：5 シ：3
- コ：3 サ：4 シ：2
- コ：2 サ：5 シ：3
- コ：2 サ：4 シ：2
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問110）へ
令和4年度（2022年度）本試験 問題一覧
次の問題（問112）へ