大学入学共通テスト（数学） 過去問
令和4年度（2022年度）本試験
問110 (数学Ⅱ・数学B（第5問） 問6)
問題文
空欄（ ク／ケ ）に当てはまるものを選べ。 
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
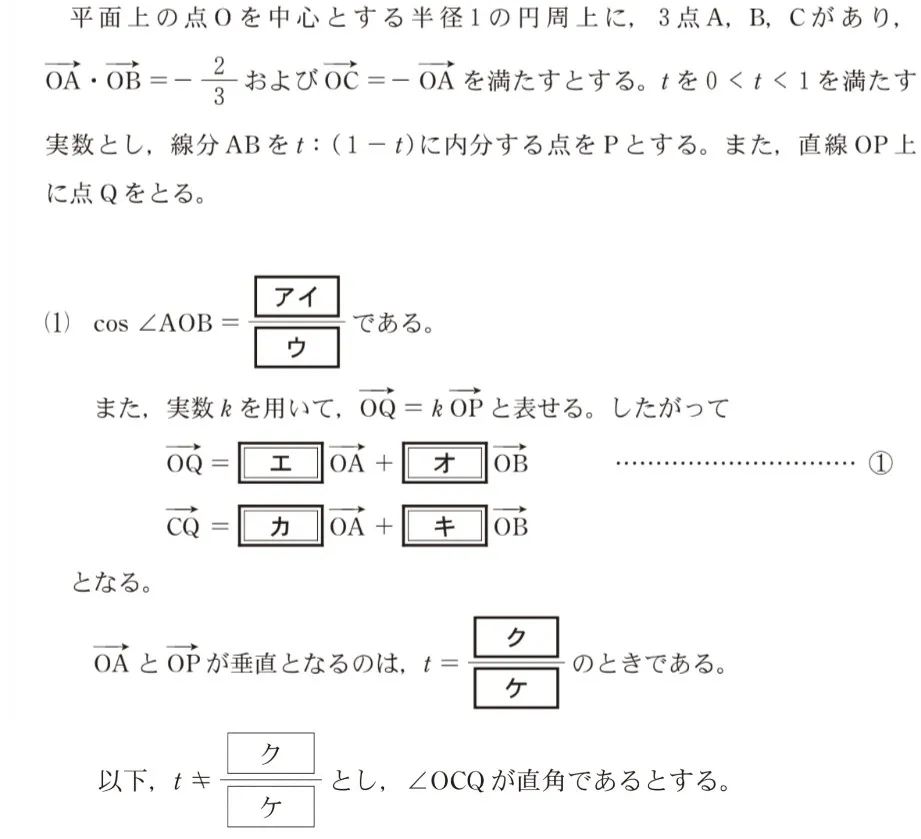
大学入学共通テスト（数学）試験 令和4年度（2022年度）本試験 問110（数学Ⅱ・数学B（第5問） 問6） （訂正依頼・報告はこちら）
空欄（ ク／ケ ）に当てはまるものを選べ。
- 1／3
- 2／4
- 3／5
- 4／6
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問109）へ
令和4年度（2022年度）本試験 問題一覧
次の問題（問111）へ