大学入学共通テスト（数学） 過去問
令和4年度（2022年度）追・再試験
問122 (数学Ⅱ・数学B（第5問） 問5)
問題文
以下（ ケ ）・（ コ ）にあてはまる組み合わせとして正しいものを選べ。
aを正の実数とする。Oを原点とする座標空間に4点
A1（1，0，a）、A2（0，1，a）、A3（−1，0，a）、A4（0，−1，a）がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
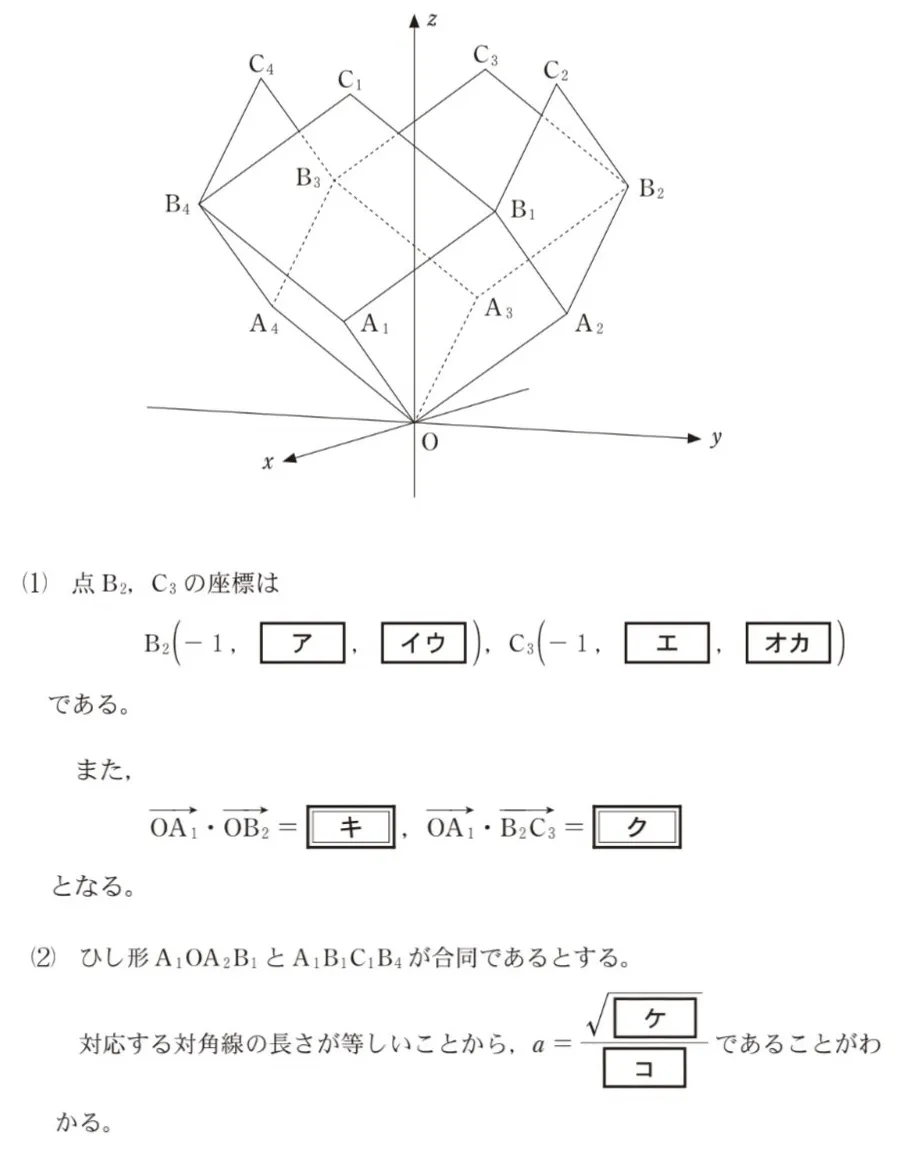
aを正の実数とする。Oを原点とする座標空間に4点
A1（1，0，a）、A2（0，1，a）、A3（−1，0，a）、A4（0，−1，a）がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）追・再試験 問122（数学Ⅱ・数学B（第5問） 問5） （訂正依頼・報告はこちら）
以下（ ケ ）・（ コ ）にあてはまる組み合わせとして正しいものを選べ。
aを正の実数とする。Oを原点とする座標空間に4点
A1（1，0，a）、A2（0，1，a）、A3（−1，0，a）、A4（0，−1，a）がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
aを正の実数とする。Oを原点とする座標空間に4点
A1（1，0，a）、A2（0，1，a）、A3（−1，0，a）、A4（0，−1，a）がある。また、次の図のように、4点B1、B2、B3、B4を四角形A1OA2B1、A2OA3B2、A3OA4B3、A4OA1B4がそれぞれひし形になるようにとる。さらに、4点C1、C2、C3、C4を四角形A1B1C1B4、A2B2C2B1、A3B3C3B2、A4B4C4B3がそれぞれひし形になるようにとる。
ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
- ケ：2 コ：2
- ケ：2 コ：3
- ケ：3 コ：4
- ケ：3 コ：5
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
a=√2/2なので、正解です。
a=√2/2なので、不正解です。
a=√2/2なので、不正解です。
a=√2/2なので、不正解です。
対角線の組み合わせの数を考慮することがpointです。
参考になった数0
この解説の修正を提案する
前の問題（問121）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問123）へ