大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問48 (数学Ⅰ・数学A(第5問) 問8)
問題文
<手順2>
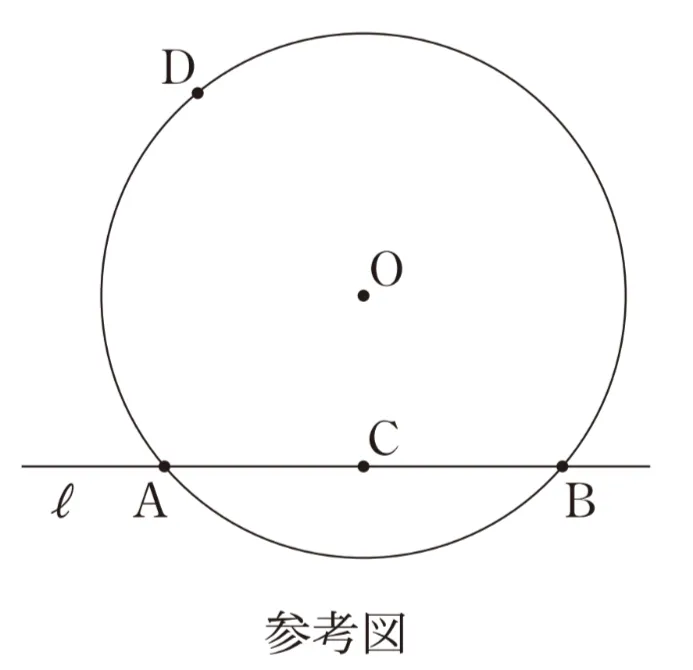
(Step1)円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step2)円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step3)点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step4)点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS=( キ )である。
円Oの半径が√5で、OT=3√6であったとすると、3点O、P、Rを通る円の半径は
( ク )√( ケ )/( コ )であり、RT=( サ )である。
( サ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問48(数学Ⅰ・数学A(第5問) 問8) (訂正依頼・報告はこちら)
<手順2>
(Step1)円Oと共有点をもたない直線lを引く。中心Oから直線lに垂直な直線を引き、直線lとの交点をPとする。
(Step2)円Oの周上に、点Qを∠POQが鈍角となるようにとる。直線PQを引き、円Oとの交点でQとは異なる点をRとする。
(Step3)点Qを通り直線OPに垂直な直線を引き、円Oとの交点でQとは異なる点をSとする。
(Step4)点Sにおける円Oの接線を引き、直線lとの交点をTとする。
このとき、∠PTS=( キ )である。
円Oの半径が√5で、OT=3√6であったとすると、3点O、P、Rを通る円の半径は
( ク )√( ケ )/( コ )であり、RT=( サ )である。
( サ )にあてはまるものを次のうちから1つ選べ。

- 6
- 7
- 8
- 9
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問47)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問49)へ