大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問96 (数学Ⅱ・数学B(第4問) 問6)
問題文
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金をan万円とおく。ただし、p>0とし、nは自然数とする。
例えば、a1=10+p、a2=1.01(10+p)+pである。
(1)anを求めるために二つの方針で考える。
<方針1>
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金a3万円について、a3=( ア )である。すべての自然数nについて
an+1=( イ )an+( ウ )
が成り立つ。これは
an+1+( エ )=( オ )(an+[ エ ])
と変形でき、anを求めることができる。
<方針2>
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
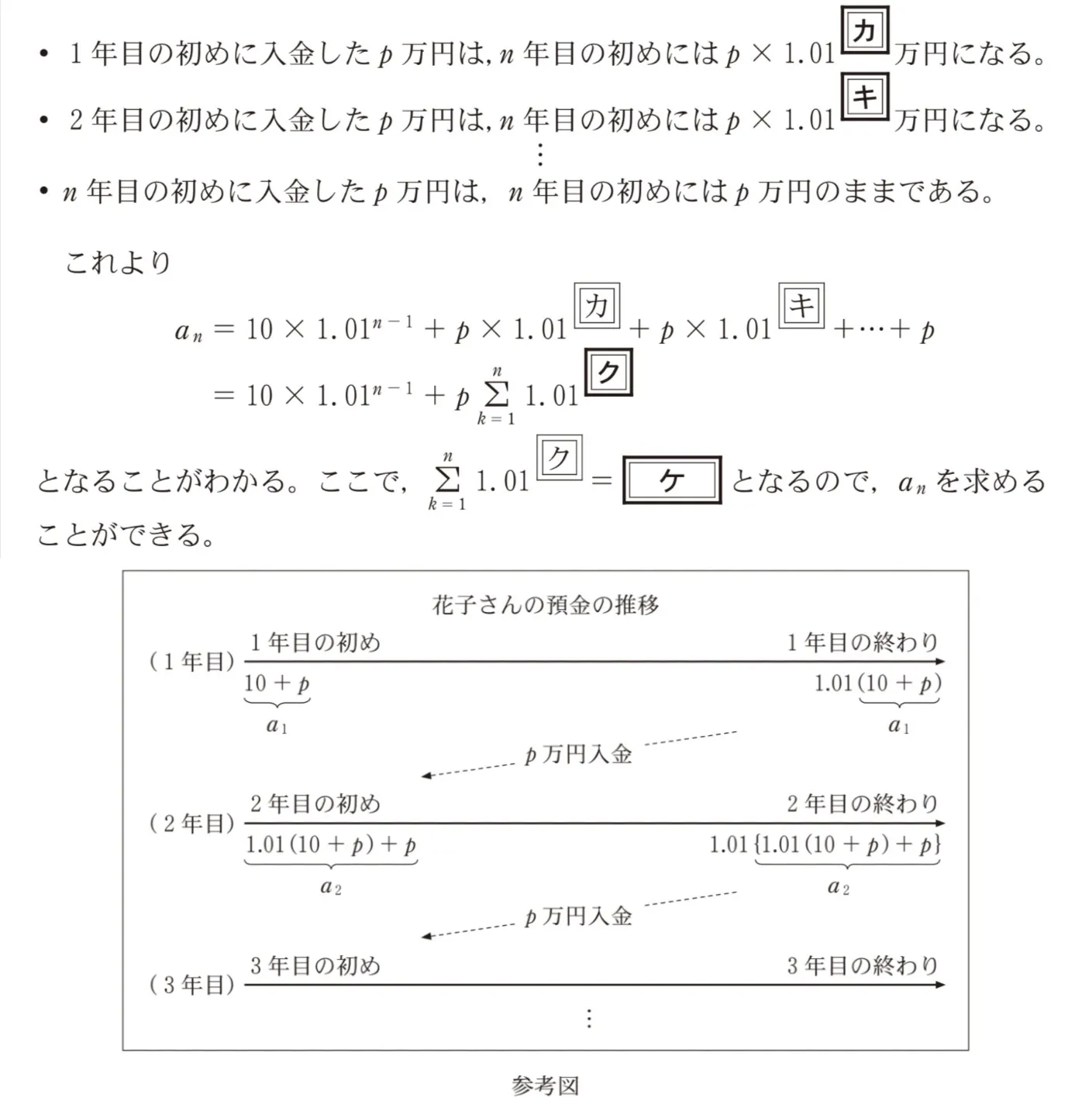
もともと預金口座にあった10万円は、2年目の初めには10✕1.01万円になり、3年目の初めには10✕1.012万円になる。同様に考えるとn年目の初めには10✕1.01n−1万円になる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問96(数学Ⅱ・数学B(第4問) 問6) (訂正依頼・報告はこちら)
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金をan万円とおく。ただし、p>0とし、nは自然数とする。
例えば、a1=10+p、a2=1.01(10+p)+pである。
(1)anを求めるために二つの方針で考える。
<方針1>
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金a3万円について、a3=( ア )である。すべての自然数nについて
an+1=( イ )an+( ウ )
が成り立つ。これは
an+1+( エ )=( オ )(an+[ エ ])
と変形でき、anを求めることができる。
<方針2>
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
もともと預金口座にあった10万円は、2年目の初めには10✕1.01万円になり、3年目の初めには10✕1.012万円になる。同様に考えるとn年目の初めには10✕1.01n−1万円になる。

- n+1
- n
- n−1
- n−2
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
1年目の初めに入金したp万円は
10万円の時と同様にn年めの初めには
p×1.01n-1万円になります。
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
この解答は導出の手順・計算結果ともに正しく、論理的に正しいです。
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
参考になった数0
この解説の修正を提案する
前の問題(問95)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問97)へ