大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問152 (情報関係基礎(第3問) 問9)
問題文
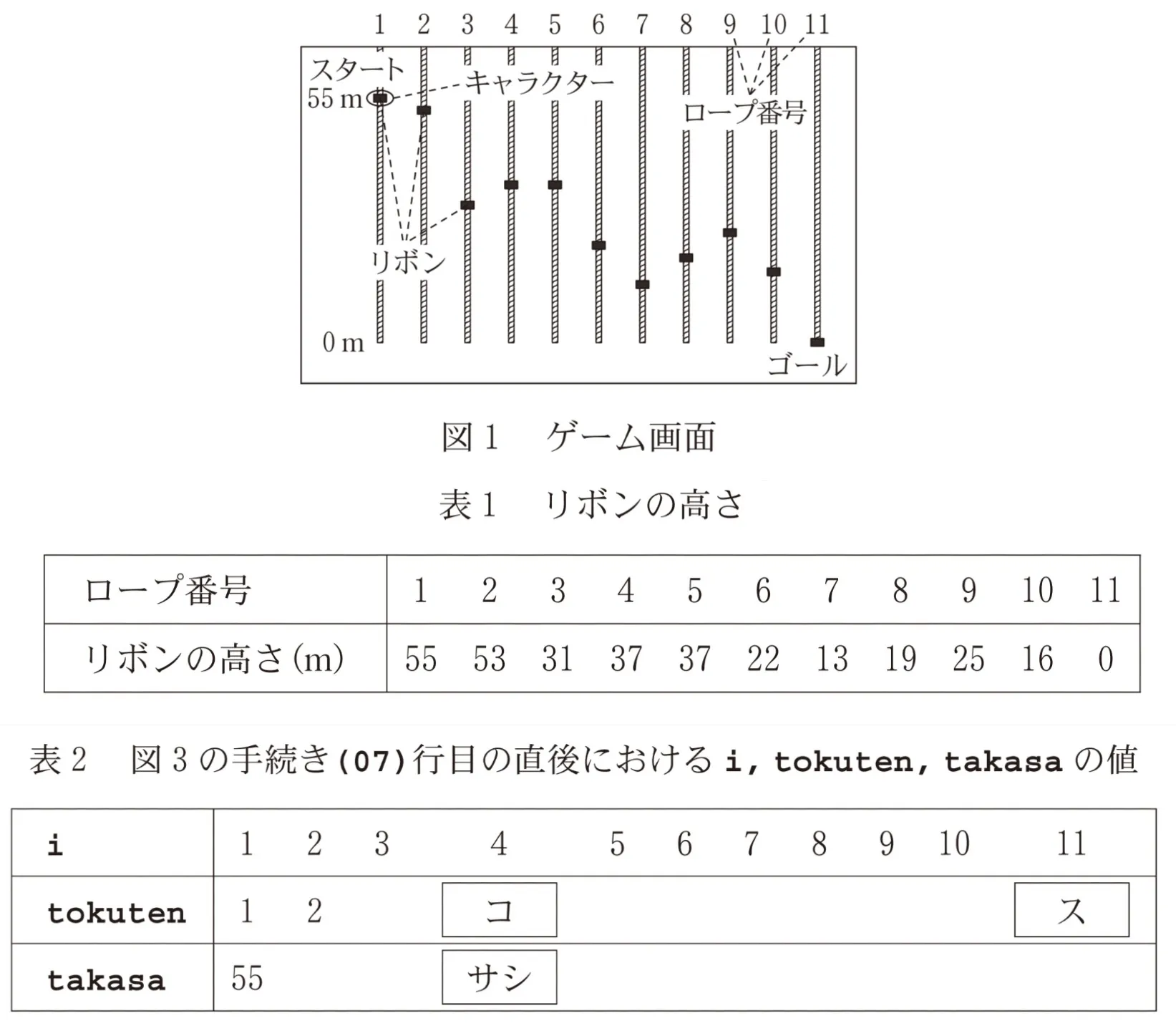
Aさんは、天井から地上まで吊り下げられたロープをキャラクターに順次飛び移らせてゴールを目指すゲーム(図1)を遊んでいる。ロープは全部で11本あり、一列に並んでいる。ゲームはキャラクターが1本目のロープの高さ55mの地点にいる状況から始まり、11本目のロープの高さ0mの地点がゴールである。キャラクターができることは、ロープを降りることと、同じ高さのまま次のロープに飛び移ることの二つのみであり、ロープを登ったり、前のロープに戻ったりすることはできない。各ロープには1か所ずつリボンが巻かれており、キャラクターがこのリボンに触れるたびに得点を1点獲得できる。各ロープにリボンが巻かれている高さ(以下、リボンの高さと呼ぶ。)はあらかじめ決まっており、表1のとおりとなっている。ゴールに到達して最後のリボンの得点を加えたゲーム終了時の得点をできるだけ高くするため、Aさんは手続きを作成して、どのようにキャラクターを動かしたらよいか検討することにした。
(1)Aさんは手始めとして、全部で11本のロープで合計55m降りるのだから、各ロープを5mずつ降りるという動かし方を考えた。このゲームはロープの降り始めや降り終わりでもリボンに触れたとみなすので、1本目のロープで55mから50mまで降りるときは、55mの高さのリボンに触れたこととなり、1点獲得できる。2本目では50mから45mまで降りるが、ここではリボンに触れない。また、6本目では( アイ )mから( ウエ )mまで降りるが、ここでもリボンに触れない。
この動かし方での得点を求めるためにAさんが作成した手続きが図2である。なお、各ロープにおけるリボンの高さは配列Ribonに格納されており、Ribon[i]はi本目のロープのリボンの高さを表す。また、変数tokutenには得点を、変数takasaにはキャラクターが今いる高さを格納する。手続きを実行し、ゲーム終了時の得点は( キ )点であることがわかった。
図2 5mずつ降りるときの得点を求める手続き
(01)tokuten←0
(02)takasa←55
(03)iを1から11まで1ずつ増やしながら,
(04)│ もし( オ )ならば
(05)│ │ tokuten←tokutenn+1
(06)│ を実行する
(07)│ takasa←( カ )
(08)を繰り返す
(09)「得点は」とtokutenと「点」を表示する
(2)Aさんは、(1)の動かし方では1本目のロープでリボンに触れた後に5m降りたことで、2本目のロープのリボンに触れ損ねて損をしていることに気がついた。そこでAさんは毎回5m降りるという動かし方をやめ、次の新しい動かし方を考えた。
【新しい動かし方】
キャラクターが今いるロープでリボンに触れることができるときは、リボンの高さまで降りてリボンに触れた後に次のロープに飛び移る。そうでないときは、ロープを降りずにそのまま次のロープに飛び移る。これを最後のロープまで順次繰り返す。
この動かし方での得点を求めるために作成した手続きが図3である。
図3 新しい動かし方での得点を求める手続き
(01)tokuten←0
(02)takasa←55
(03)iを1から11まで1ずつ増やしながら,
(04)│ もし( ク )ならば
(05)│ │ tokuten←tokutenn+1
(06)│ takasa←( ケ )
(07)│ を実行する
(08)を繰り返す
(09)「得点は」とtokutenと「点」を表示する
手続きの流れを確認するため、表2を用意して、図3の(07)行目の直後におけるi,tokuten,takasaの値を記録した。その結果、i=4のときのtokutenの値は( コ )、takasaの値は( サシ )であった。手続きを実行し、ゲーム終了時の得点は( ス )点であることがわかった。
表2を眺めていてAさんは、あるロープで降りすぎると、その後の複数のロープのリボンに触れ損ねて損をすることがあると気がついた。そこで、新たに定数GENDO(単位はm)を導入し、リボンに触れるためにGENDOm以上降りる必要があるときはロープを降りずにそのまま次のロープに飛び移るように動かし方を改めることにした。ただし、最後のロープではリボンの高さである0mまで必ず降りることとする。試しにAさんはGENDOの値を20としたうえで、図3の(04)行目の( ク )を( セ )と書き換えて手続きを実行した。その結果、ゲーム終了時の得点は( ソ )点となることがわかった。
( サシ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問152(情報関係基礎(第3問) 問9) (訂正依頼・報告はこちら)
Aさんは、天井から地上まで吊り下げられたロープをキャラクターに順次飛び移らせてゴールを目指すゲーム(図1)を遊んでいる。ロープは全部で11本あり、一列に並んでいる。ゲームはキャラクターが1本目のロープの高さ55mの地点にいる状況から始まり、11本目のロープの高さ0mの地点がゴールである。キャラクターができることは、ロープを降りることと、同じ高さのまま次のロープに飛び移ることの二つのみであり、ロープを登ったり、前のロープに戻ったりすることはできない。各ロープには1か所ずつリボンが巻かれており、キャラクターがこのリボンに触れるたびに得点を1点獲得できる。各ロープにリボンが巻かれている高さ(以下、リボンの高さと呼ぶ。)はあらかじめ決まっており、表1のとおりとなっている。ゴールに到達して最後のリボンの得点を加えたゲーム終了時の得点をできるだけ高くするため、Aさんは手続きを作成して、どのようにキャラクターを動かしたらよいか検討することにした。
(1)Aさんは手始めとして、全部で11本のロープで合計55m降りるのだから、各ロープを5mずつ降りるという動かし方を考えた。このゲームはロープの降り始めや降り終わりでもリボンに触れたとみなすので、1本目のロープで55mから50mまで降りるときは、55mの高さのリボンに触れたこととなり、1点獲得できる。2本目では50mから45mまで降りるが、ここではリボンに触れない。また、6本目では( アイ )mから( ウエ )mまで降りるが、ここでもリボンに触れない。
この動かし方での得点を求めるためにAさんが作成した手続きが図2である。なお、各ロープにおけるリボンの高さは配列Ribonに格納されており、Ribon[i]はi本目のロープのリボンの高さを表す。また、変数tokutenには得点を、変数takasaにはキャラクターが今いる高さを格納する。手続きを実行し、ゲーム終了時の得点は( キ )点であることがわかった。
図2 5mずつ降りるときの得点を求める手続き
(01)tokuten←0
(02)takasa←55
(03)iを1から11まで1ずつ増やしながら,
(04)│ もし( オ )ならば
(05)│ │ tokuten←tokutenn+1
(06)│ を実行する
(07)│ takasa←( カ )
(08)を繰り返す
(09)「得点は」とtokutenと「点」を表示する
(2)Aさんは、(1)の動かし方では1本目のロープでリボンに触れた後に5m降りたことで、2本目のロープのリボンに触れ損ねて損をしていることに気がついた。そこでAさんは毎回5m降りるという動かし方をやめ、次の新しい動かし方を考えた。
【新しい動かし方】
キャラクターが今いるロープでリボンに触れることができるときは、リボンの高さまで降りてリボンに触れた後に次のロープに飛び移る。そうでないときは、ロープを降りずにそのまま次のロープに飛び移る。これを最後のロープまで順次繰り返す。
この動かし方での得点を求めるために作成した手続きが図3である。
図3 新しい動かし方での得点を求める手続き
(01)tokuten←0
(02)takasa←55
(03)iを1から11まで1ずつ増やしながら,
(04)│ もし( ク )ならば
(05)│ │ tokuten←tokutenn+1
(06)│ takasa←( ケ )
(07)│ を実行する
(08)を繰り返す
(09)「得点は」とtokutenと「点」を表示する
手続きの流れを確認するため、表2を用意して、図3の(07)行目の直後におけるi,tokuten,takasaの値を記録した。その結果、i=4のときのtokutenの値は( コ )、takasaの値は( サシ )であった。手続きを実行し、ゲーム終了時の得点は( ス )点であることがわかった。
表2を眺めていてAさんは、あるロープで降りすぎると、その後の複数のロープのリボンに触れ損ねて損をすることがあると気がついた。そこで、新たに定数GENDO(単位はm)を導入し、リボンに触れるためにGENDOm以上降りる必要があるときはロープを降りずにそのまま次のロープに飛び移るように動かし方を改めることにした。ただし、最後のロープではリボンの高さである0mまで必ず降りることとする。試しにAさんはGENDOの値を20としたうえで、図3の(04)行目の( ク )を( セ )と書き換えて手続きを実行した。その結果、ゲーム終了時の得点は( ソ )点となることがわかった。
( サシ )にあてはまるものを次のうちから1つ選べ。

- 21
- 31
- 41
- 51
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問151)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問153)へ