大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問156 (情報関係基礎(第3問) 問13)
問題文
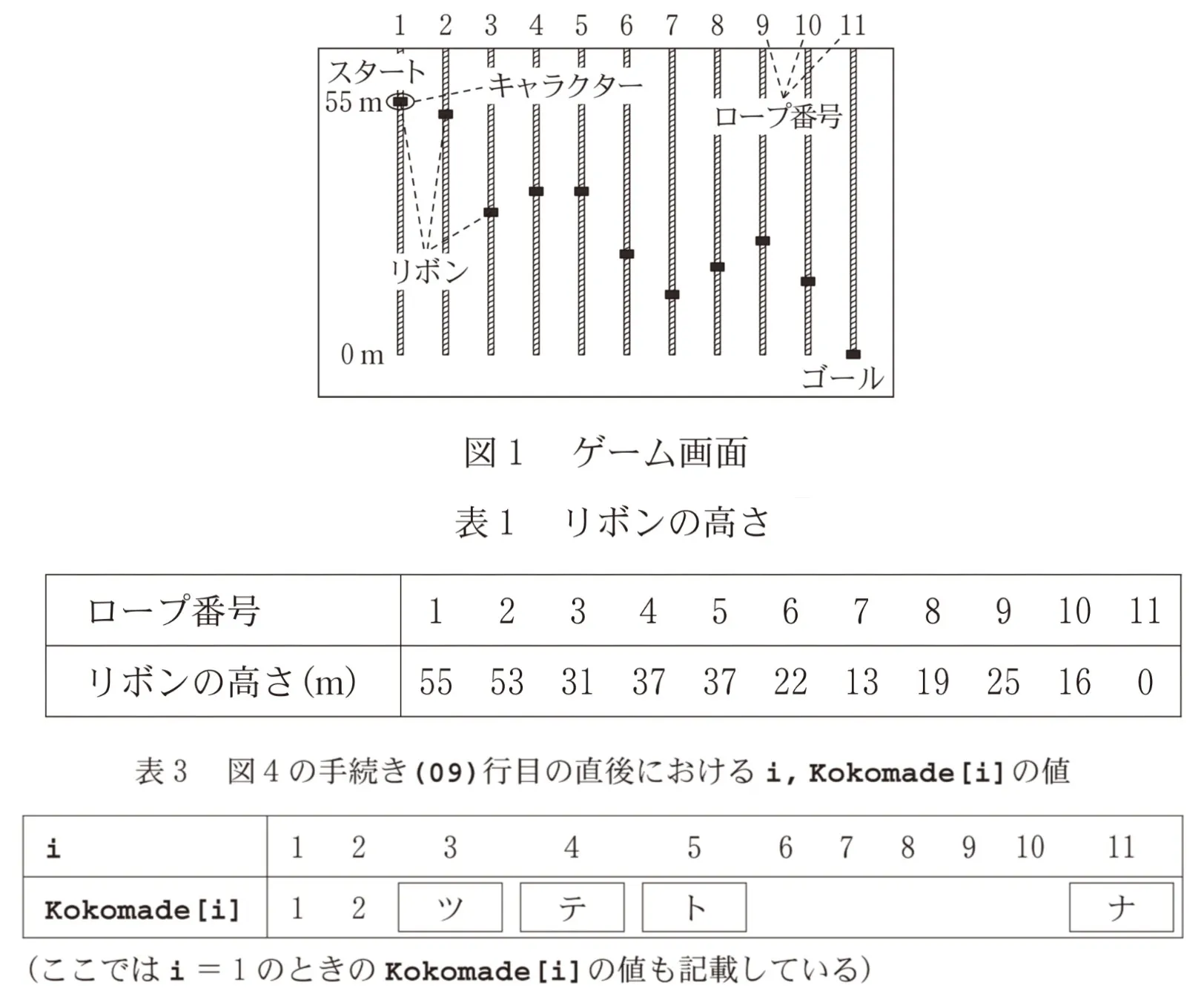
Aさんは、天井から地上まで吊り下げられたロープをキャラクターに順次飛び移らせてゴールを目指すゲーム(図1)を遊んでいる。ロープは全部で11本あり、一列に並んでいる。ゲームはキャラクターが1本目のロープの高さ55mの地点にいる状況から始まり、11本目のロープの高さ0mの地点がゴールである。キャラクターができることは、ロープを降りることと、同じ高さのまま次のロープに飛び移ることの二つのみであり、ロープを登ったり、前のロープに戻ったりすることはできない。各ロープには1か所ずつリボンが巻かれており、キャラクターがこのリボンに触れるたびに得点を1点獲得できる。各ロープにリボンが巻かれている高さ(以下、リボンの高さと呼ぶ。)はあらかじめ決まっており、表1のとおりとなっている。ゴールに到達して最後のリボンの得点を加えたゲーム終了時の得点をできるだけ高くするため、Aさんは手続きを作成して、どのようにキャラクターを動かしたらよいか検討することにした。
(3)Aさんはこのゲームで獲得可能な最高得点を求めるため、次の手順を考えた。まず、1本目からi本目のロープまでに限定して考え、しかもi本目のロープのリボンには必ず触れることとする。このとき獲得可能な最高得点をKokomade[i]点とする。
i=1のとき、このゲームでは1本目のロープのリボンの高さが55mでスタート地点と一致しているので、Kokomade[1]の値は1である。i≧2のときは、iより小さいすべてのt(ただしt≧1)についてKokomade[t]が求まっていれば、次のように考えてKokomade[i]を求めることができる。
【Kokomade[i]の求め方】 t本目のロープのリボンに触れて、かつi本目のロープのリボンにも触れることができる条件は、( タ )であるが、その条件を満たすすべてのtの中で、Kokomade[t]の値が最も大きいものを選ぶと、「i本目のロープのリボンに触れる一つ前に触れておくべきリボン」が定まる。すると、そのKokomade[t]の値にもとづいて、Kokomade[i]の値が定まる。
iの値を2から順次増やしていけば、すべてのiについてKokomade[i]の値を求めることができる。最後のロープのリボンの高さは0mなのでこのリボンには必ず触れることができることを考えると、Kokomade[11]がこのゲームで獲得可能な最高得点となる。この手順を考えたAさんが作成した手続きが図4である。
手続きの流れを確認するため、表3を用意して、図4の(09)行目の直後におけるi,Kokomade[i]の値を記録した。i=2のときは、2より小さいtは1のみであり、しかもこのとき条件( タ )を満たす。つまり1本目と2本目の両方のロープのリボンに触れることができるので、Kokomade[2]の値は2となる。同様に記録を続けると、i=3,4,5のときのKokomade[i]の値はそれぞれ( ツ ),( テ ),( ト )となる。手続きを実行し、このゲームで獲得可能な最高得点は( ナ )点であることがわかった。
図4 獲得可能な最高得点を求める手続き
(01)Kokomade[1]←1
(02)iを2から11まで1ずつ増やしながら,
(03)│ saikou←0
(04)│ tを1からi−1まで1ずつ増やしながら,
(05)│ │ もし( タ )かつsaikou<Kokomade[t]ならば
(06)│ │ │ saikou←Kokomade[t]
(07)│ │ を実行する
(08)│ を繰り返す
(09)│ Kokomade[i]←( チ )
(10)を繰り返す
(11)「獲得可能な最高得点は」とKokomade[11]と「点」を表示する
( タ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問156(情報関係基礎(第3問) 問13) (訂正依頼・報告はこちら)
Aさんは、天井から地上まで吊り下げられたロープをキャラクターに順次飛び移らせてゴールを目指すゲーム(図1)を遊んでいる。ロープは全部で11本あり、一列に並んでいる。ゲームはキャラクターが1本目のロープの高さ55mの地点にいる状況から始まり、11本目のロープの高さ0mの地点がゴールである。キャラクターができることは、ロープを降りることと、同じ高さのまま次のロープに飛び移ることの二つのみであり、ロープを登ったり、前のロープに戻ったりすることはできない。各ロープには1か所ずつリボンが巻かれており、キャラクターがこのリボンに触れるたびに得点を1点獲得できる。各ロープにリボンが巻かれている高さ(以下、リボンの高さと呼ぶ。)はあらかじめ決まっており、表1のとおりとなっている。ゴールに到達して最後のリボンの得点を加えたゲーム終了時の得点をできるだけ高くするため、Aさんは手続きを作成して、どのようにキャラクターを動かしたらよいか検討することにした。
(3)Aさんはこのゲームで獲得可能な最高得点を求めるため、次の手順を考えた。まず、1本目からi本目のロープまでに限定して考え、しかもi本目のロープのリボンには必ず触れることとする。このとき獲得可能な最高得点をKokomade[i]点とする。
i=1のとき、このゲームでは1本目のロープのリボンの高さが55mでスタート地点と一致しているので、Kokomade[1]の値は1である。i≧2のときは、iより小さいすべてのt(ただしt≧1)についてKokomade[t]が求まっていれば、次のように考えてKokomade[i]を求めることができる。
【Kokomade[i]の求め方】 t本目のロープのリボンに触れて、かつi本目のロープのリボンにも触れることができる条件は、( タ )であるが、その条件を満たすすべてのtの中で、Kokomade[t]の値が最も大きいものを選ぶと、「i本目のロープのリボンに触れる一つ前に触れておくべきリボン」が定まる。すると、そのKokomade[t]の値にもとづいて、Kokomade[i]の値が定まる。
iの値を2から順次増やしていけば、すべてのiについてKokomade[i]の値を求めることができる。最後のロープのリボンの高さは0mなのでこのリボンには必ず触れることができることを考えると、Kokomade[11]がこのゲームで獲得可能な最高得点となる。この手順を考えたAさんが作成した手続きが図4である。
手続きの流れを確認するため、表3を用意して、図4の(09)行目の直後におけるi,Kokomade[i]の値を記録した。i=2のときは、2より小さいtは1のみであり、しかもこのとき条件( タ )を満たす。つまり1本目と2本目の両方のロープのリボンに触れることができるので、Kokomade[2]の値は2となる。同様に記録を続けると、i=3,4,5のときのKokomade[i]の値はそれぞれ( ツ ),( テ ),( ト )となる。手続きを実行し、このゲームで獲得可能な最高得点は( ナ )点であることがわかった。
図4 獲得可能な最高得点を求める手続き
(01)Kokomade[1]←1
(02)iを2から11まで1ずつ増やしながら,
(03)│ saikou←0
(04)│ tを1からi−1まで1ずつ増やしながら,
(05)│ │ もし( タ )かつsaikou<Kokomade[t]ならば
(06)│ │ │ saikou←Kokomade[t]
(07)│ │ を実行する
(08)│ を繰り返す
(09)│ Kokomade[i]←( チ )
(10)を繰り返す
(11)「獲得可能な最高得点は」とKokomade[11]と「点」を表示する
( タ )にあてはまるものを次のうちから1つ選べ。

- Ribon[t]<Ribon[i]
- Ribon[t]>Ribon[i]
- Ribon[t]≦Ribon[i]
- Ribon[t]≧Ribon[i]
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問155)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問157)へ