大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問82 (数学Ⅱ・数学B(第3問) 問1)
問題文
( ア )にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
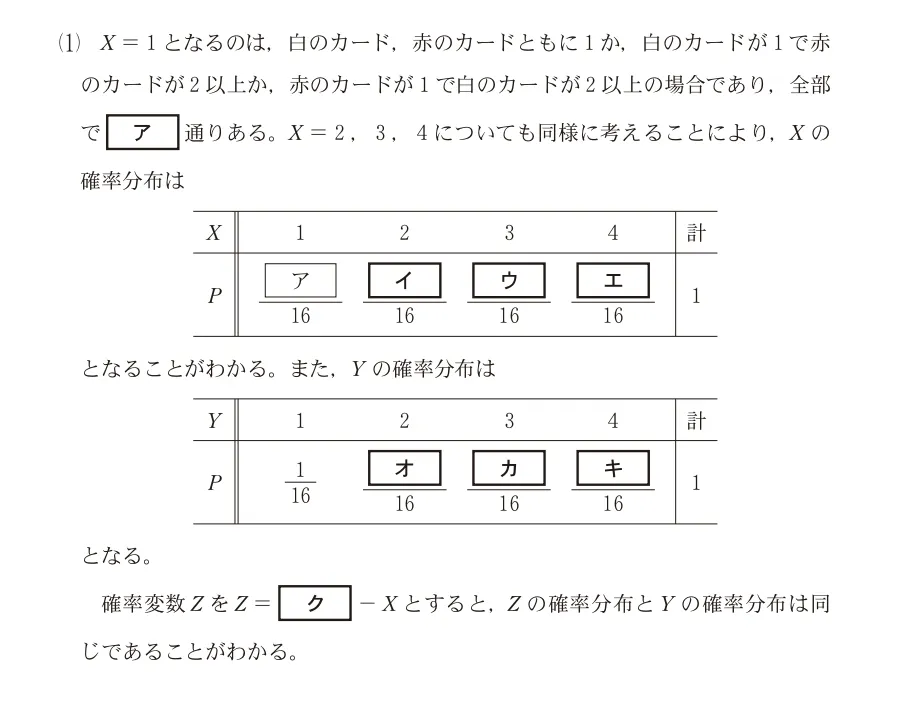
1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の白のカードが箱Aに、1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の赤のカードが箱Bに入っている。箱A、Bからそれぞれ1枚ずつのカードを無作為に取り出し、取り出したカードの数字を確認してからもとに戻す試行について、次のように確率変数X、Yを定める。
「確率変数X」
取り出した白のカードに書かれた数と赤のカードに書かれた数の小さい方の数(書かれた数が等しい場合はその数)をXの値とする。
「確率変数Y」
取り出した白のカードに書かれた数と赤のカードに書かれた数の大きい方の数(書かれた数が等しい場合はその数)をYの値とする。
太郎さんは、この試行を2回繰り返したときに記録された2個の数の平均値t2=2.50と、100回繰り返したときに記録された100個の数の平均値t100=2.95が書いてあるメモを見つけた。メモに関する太郎さんの記憶は次のとおりである。
<太郎さんの記憶>
メモに書かれていたt2とt100は「確率変数X」の平均値である。
太郎さんは、このメモに書かれていたt2とt100が「確率変数X」か「確率変数Y」のうちどちらか一方の平均値であったことは覚えていたが、太郎さんの記憶における
「確率変数X」の部分が確かでなく、もしかしたら「確率変数Y」だったかもしれないと感じている。このことについて、太郎さんが花子さんに相談したところ、花子さんは、太郎さんが見つけたメモに書かれていた二つの平均値をもとにして太郎さんの記憶が正しいかどうかがわかるのではないかと考えた。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問82(数学Ⅱ・数学B(第3問) 問1) (訂正依頼・報告はこちら)
( ア )にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の白のカードが箱Aに、1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の赤のカードが箱Bに入っている。箱A、Bからそれぞれ1枚ずつのカードを無作為に取り出し、取り出したカードの数字を確認してからもとに戻す試行について、次のように確率変数X、Yを定める。
「確率変数X」
取り出した白のカードに書かれた数と赤のカードに書かれた数の小さい方の数(書かれた数が等しい場合はその数)をXの値とする。
「確率変数Y」
取り出した白のカードに書かれた数と赤のカードに書かれた数の大きい方の数(書かれた数が等しい場合はその数)をYの値とする。
太郎さんは、この試行を2回繰り返したときに記録された2個の数の平均値t2=2.50と、100回繰り返したときに記録された100個の数の平均値t100=2.95が書いてあるメモを見つけた。メモに関する太郎さんの記憶は次のとおりである。
<太郎さんの記憶>
メモに書かれていたt2とt100は「確率変数X」の平均値である。
太郎さんは、このメモに書かれていたt2とt100が「確率変数X」か「確率変数Y」のうちどちらか一方の平均値であったことは覚えていたが、太郎さんの記憶における
「確率変数X」の部分が確かでなく、もしかしたら「確率変数Y」だったかもしれないと感じている。このことについて、太郎さんが花子さんに相談したところ、花子さんは、太郎さんが見つけたメモに書かれていた二つの平均値をもとにして太郎さんの記憶が正しいかどうかがわかるのではないかと考えた。

- 4
- 5
- 6
- 7
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
リード文が長いため、読んでいる途中で問題設定の勘違いが起こらないように気を付けながら読みましょう。
箱Aには白の1,2,3,4が、箱Bには赤の1,2,3,4が入っています。
例えば一回目の試行でAからは2、Bからは4が出た場合、X=2,Y=4となります。
(試験を解く際は、このように自分の中で簡単な実験を交えつつ問題文を把握していくとよいでしょう。)
また、リード文後半のt100=2.95という情報と確率変数の定め方から、太郎さんの記憶は間違っていて、
メモに書かれていたt2とt100は「確率変数Y」の平均値である。
のほうが正しいのではないかという予測が立ちます。
(あくまで予測が立つだけで、その予測に妥当性があるかどうかを検証するのが統計です)
それでは以上のことを踏まえて問題を見ていきましょう。
(1)
この先の穴埋めを眺めると、確率を一つ一つ計算するのではなく、起こりうる場合の数を求めてしまったほうが良さそうです。
そこで、横に箱Aから取り出した数字を書き、縦に箱Bから取り出した数字を書いた票を作り、それぞれの場合においてXがどのような値になるかを書き込みます。
この表を作ってしまえば、あとはこの表の中でX=k(k=1,2,3,4)となる場合の数を数えれば良いですね。
よって、アに入るのは7と分かります。
アは7より
誤
アは7より
誤
アは7より
誤
アは7より
正
確率や統計といった分野では問題文の設定の正しい把握が最も重要です。
焦らずにしっかりと目を通しましょう。
参考になった数0
この解説の修正を提案する
前の問題(問81)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問83)へ