大学入学共通テスト(数学) 過去問
令和5年度(2023年度)追・再試験
問83 (数学Ⅱ・数学B(第3問) 問2)
問題文
( イ )・( ウ )・( エ )にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の白のカードが箱Aに、1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の赤のカードが箱Bに入っている。箱A、Bからそれぞれ1枚ずつのカードを無作為に取り出し、取り出したカードの数字を確認してからもとに戻す試行について、次のように確率変数X、Yを定める。
「確率変数X」
取り出した白のカードに書かれた数と赤のカードに書かれた数の小さい方の数(書かれた数が等しい場合はその数)をXの値とする。
「確率変数Y」
取り出した白のカードに書かれた数と赤のカードに書かれた数の大きい方の数(書かれた数が等しい場合はその数)をYの値とする。
太郎さんは、この試行を2回繰り返したときに記録された2個の数の平均値t2=2.50と、100回繰り返したときに記録された100個の数の平均値t100=2.95が書いてあるメモを見つけた。メモに関する太郎さんの記憶は次のとおりである。
<太郎さんの記憶>
メモに書かれていたt2とt100は「確率変数X」の平均値である。
太郎さんは、このメモに書かれていたt2とt100が「確率変数X」か「確率変数Y」のうちどちらか一方の平均値であったことは覚えていたが、太郎さんの記憶における
「確率変数X」の部分が確かでなく、もしかしたら「確率変数Y」だったかもしれないと感じている。このことについて、太郎さんが花子さんに相談したところ、花子さんは、太郎さんが見つけたメモに書かれていた二つの平均値をもとにして太郎さんの記憶が正しいかどうかがわかるのではないかと考えた。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)追・再試験 問83(数学Ⅱ・数学B(第3問) 問2) (訂正依頼・報告はこちら)
( イ )・( ウ )・( エ )にあてはまるものを1つ選べ。
以下の問題を解答するにあたっては、必要に応じて 正規分布表(リンク) を用いてもよい。
1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の白のカードが箱Aに、1、2、3、4の数字がそれぞれ一つずつ書かれた4枚の赤のカードが箱Bに入っている。箱A、Bからそれぞれ1枚ずつのカードを無作為に取り出し、取り出したカードの数字を確認してからもとに戻す試行について、次のように確率変数X、Yを定める。
「確率変数X」
取り出した白のカードに書かれた数と赤のカードに書かれた数の小さい方の数(書かれた数が等しい場合はその数)をXの値とする。
「確率変数Y」
取り出した白のカードに書かれた数と赤のカードに書かれた数の大きい方の数(書かれた数が等しい場合はその数)をYの値とする。
太郎さんは、この試行を2回繰り返したときに記録された2個の数の平均値t2=2.50と、100回繰り返したときに記録された100個の数の平均値t100=2.95が書いてあるメモを見つけた。メモに関する太郎さんの記憶は次のとおりである。
<太郎さんの記憶>
メモに書かれていたt2とt100は「確率変数X」の平均値である。
太郎さんは、このメモに書かれていたt2とt100が「確率変数X」か「確率変数Y」のうちどちらか一方の平均値であったことは覚えていたが、太郎さんの記憶における
「確率変数X」の部分が確かでなく、もしかしたら「確率変数Y」だったかもしれないと感じている。このことについて、太郎さんが花子さんに相談したところ、花子さんは、太郎さんが見つけたメモに書かれていた二つの平均値をもとにして太郎さんの記憶が正しいかどうかがわかるのではないかと考えた。

- イ:3 ウ:1 エ:1
- イ:5 ウ:3 エ:1
- イ:7 ウ:5 エ:3
- イ:9 ウ:7 エ:5
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
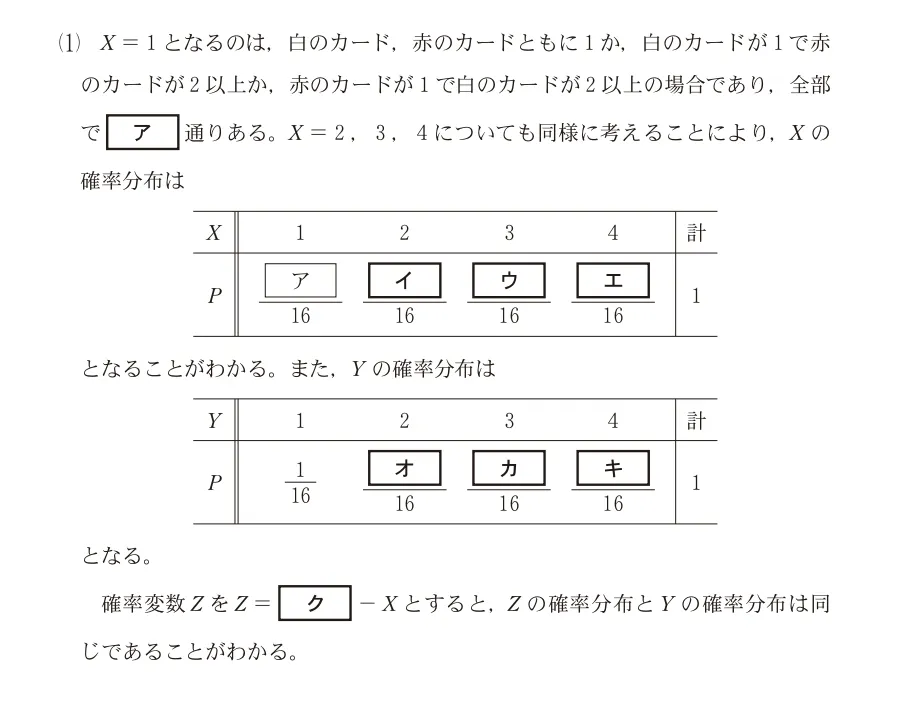
Xについての表を作り、X=2,3,4となる場合の数をそれぞれ数えていきます。
上の表から、
イに入るのは5
ウに入るのは3
エに入るのは1
と分かります。
イに入るのは5
ウに入るのは3
エに入るのは1
より誤
イに入るのは5
ウに入るのは3
エに入るのは1
より正
イに入るのは5
ウに入るのは3
エに入るのは1
より誤
イに入るのは5
ウに入るのは3
エに入るのは1
より誤
表を作って場合の数を数え上げました。
数え上げる際はケアレスミスを起こさないようにしましょう。
例えば、X=1,2,3,4をすべて足し合わせてちゃんと分母の16になるか等を確認しておくとよいでしょう。
参考になった数0
この解説の修正を提案する
前の問題(問82)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問84)へ