大学入学共通テスト（数学） 過去問
令和5年度（2023年度）追・再試験
問111 (数学Ⅱ・数学B（第4問） 問13)
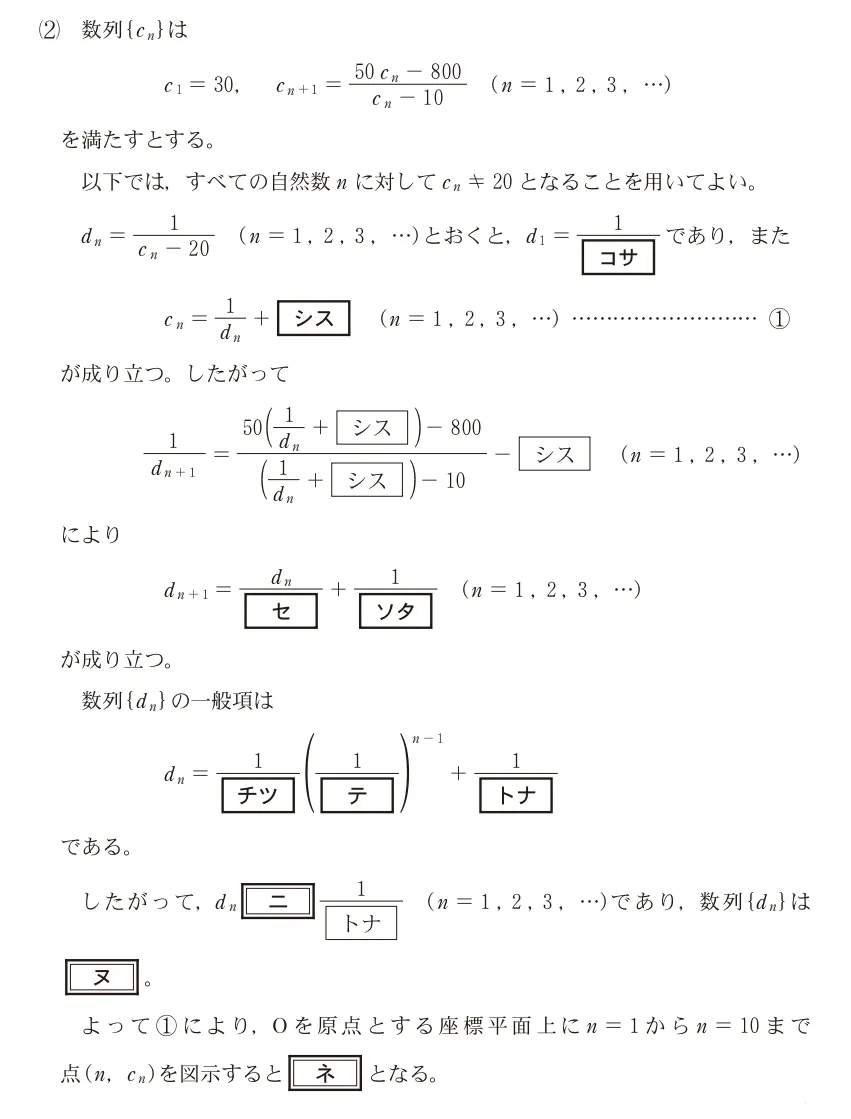
問題文
（ ネ ）について、最も適当なものを1つ選べ。
数列の増減について考える。与えられた数列｛pn｝の増減について次のように定める。
・すべての自然数nについてpn＜pn＋1となるとき、数列｛pn｝はつねに増加するという。
・すべての自然数nについてpn＞pn＋1となるとき、数列｛pn｝はつねに減少するという。
・pk＜pk＋1となる自然数kがあり、さらにpl＞pl＋1となる自然数lもあるとき、数列｛pn｝は増加することも減少することもあるという。
数列の増減について考える。与えられた数列｛pn｝の増減について次のように定める。
・すべての自然数nについてpn＜pn＋1となるとき、数列｛pn｝はつねに増加するという。
・すべての自然数nについてpn＞pn＋1となるとき、数列｛pn｝はつねに減少するという。
・pk＜pk＋1となる自然数kがあり、さらにpl＞pl＋1となる自然数lもあるとき、数列｛pn｝は増加することも減少することもあるという。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和5年度（2023年度）追・再試験 問111（数学Ⅱ・数学B（第4問） 問13） （訂正依頼・報告はこちら）
（ ネ ）について、最も適当なものを1つ選べ。
数列の増減について考える。与えられた数列｛pn｝の増減について次のように定める。
・すべての自然数nについてpn＜pn＋1となるとき、数列｛pn｝はつねに増加するという。
・すべての自然数nについてpn＞pn＋1となるとき、数列｛pn｝はつねに減少するという。
・pk＜pk＋1となる自然数kがあり、さらにpl＞pl＋1となる自然数lもあるとき、数列｛pn｝は増加することも減少することもあるという。
数列の増減について考える。与えられた数列｛pn｝の増減について次のように定める。
・すべての自然数nについてpn＜pn＋1となるとき、数列｛pn｝はつねに増加するという。
・すべての自然数nについてpn＞pn＋1となるとき、数列｛pn｝はつねに減少するという。
・pk＜pk＋1となる自然数kがあり、さらにpl＞pl＋1となる自然数lもあるとき、数列｛pn｝は増加することも減少することもあるという。
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
であり、dnは狭義単調減少数列だったので、
cnは狭義単調増加数列と分かります。
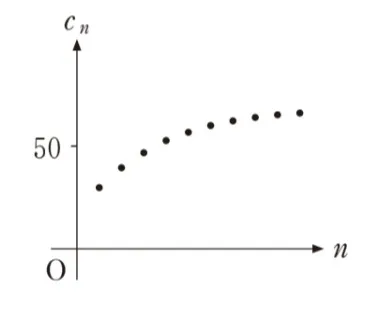
したがってまずは単調増加なグラフを選んでいきます。
また、dn>1/20より、20>1/dnですから、
cn<40がわかります。
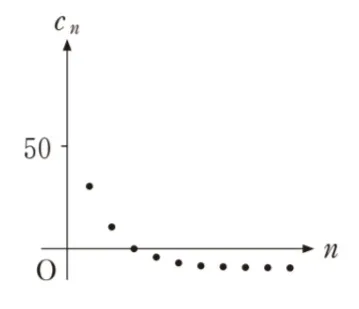
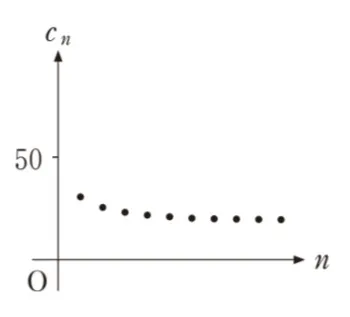
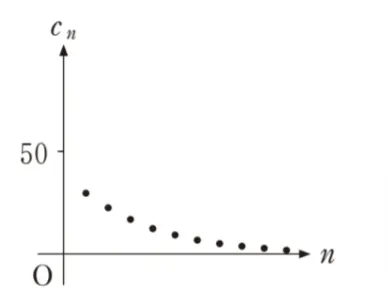
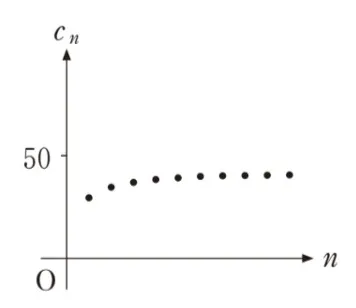
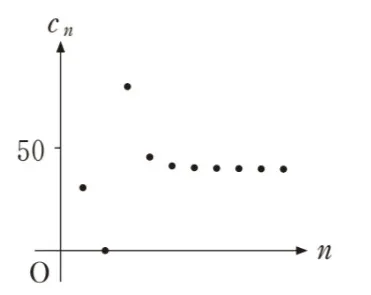
よってネに入るのは狭義単調増加かつ40未満となるグラフ です。
ネに入るのは狭義単調増加かつ40未満となるグラフ
より誤
ネに入るのは狭義単調増加かつ40未満となるグラフ
より誤
ネに入るのは狭義単調増加かつ40未満となるグラフ
より誤
ネに入るのは狭義単調増加かつ40未満となるグラフ
より誤
ネに入るのは狭義単調増加かつ40未満となるグラフ
より正
ネに入るのは狭義単調増加かつ40未満となるグラフ
より誤
思考力を問われる問題です。
dnの特徴を押さえ、それ満たすかどうかで選んでいきましょう。
参考になった数0
この解説の修正を提案する
前の問題（問110）へ
令和5年度（2023年度）追・再試験 問題一覧
次の問題（問112）へ