大学入学共通テスト（数学） 過去問
令和5年度（2023年度）追・再試験
問114 (数学Ⅱ・数学B（第5問） 問3)
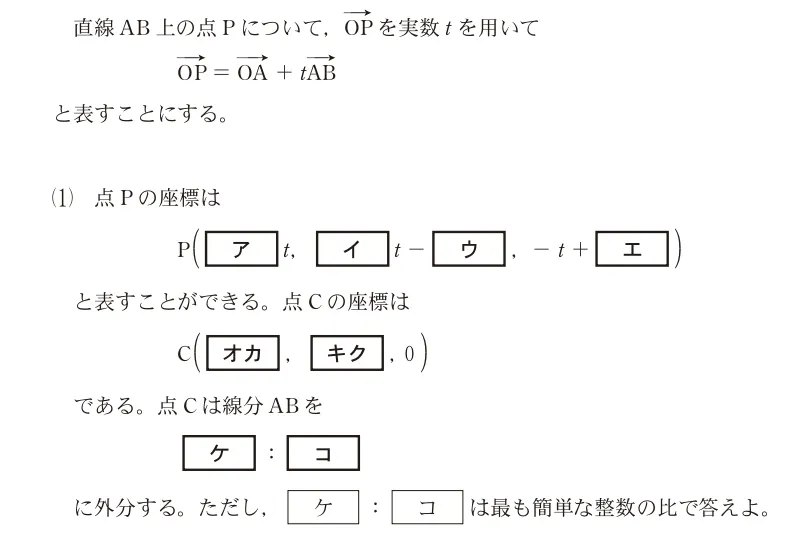
問題文
（ ケ ）・（ コ ）にあてはまるものを1つ選べ。
点Oを原点とする座標空間において2点A、Bの座標を
A（0，−3，5）， B（2，0，4）
とし、直線ABとxy平面との交点をCとする。また、点Dの座標を
D（7，4，5）
とする。
点Oを原点とする座標空間において2点A、Bの座標を
A（0，−3，5）， B（2，0，4）
とし、直線ABとxy平面との交点をCとする。また、点Dの座標を
D（7，4，5）
とする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和5年度（2023年度）追・再試験 問114（数学Ⅱ・数学B（第5問） 問3） （訂正依頼・報告はこちら）
（ ケ ）・（ コ ）にあてはまるものを1つ選べ。
点Oを原点とする座標空間において2点A、Bの座標を
A（0，−3，5）， B（2，0，4）
とし、直線ABとxy平面との交点をCとする。また、点Dの座標を
D（7，4，5）
とする。
点Oを原点とする座標空間において2点A、Bの座標を
A（0，−3，5）， B（2，0，4）
とし、直線ABとxy平面との交点をCとする。また、点Dの座標を
D（7，4，5）
とする。
- ケ：2 コ：1
- ケ：3 コ：2
- ケ：4 コ：3
- ケ：5 コ：4
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
この解説ではベクトルOAをOAのように表記します
点Cはxy平面上に存在し、点Aと点Bはz座標が正なので、
ACとBCをABを用いて表してみます。
t=5とOPの置き方より
AC＝5AB
また、
BC＝BA+AC＝-AB+5AB=4AB
よって
|AC|:|CB|=5:4
となり、CはABを5：４に外分することがわかります。
よって
ケに入るのは5
コに入るのは4
となります。
ケに入るのは5
コに入るのは4
より誤
ケに入るのは5
コに入るのは4
より誤
ケに入るのは5
コに入るのは4
より誤
ケに入るのは5
コに入るのは4
より正
図に各点を書き込むことで、ACとBCをABで表せば外分比を求められる事が分かります。
特に図形問題やベクトルの問題では、図的考察が計算短縮の鍵となるため、書き込みを積極的に行っていきましょう。
参考になった数0
この解説の修正を提案する
前の問題（問113）へ
令和5年度（2023年度）追・再試験 問題一覧
次の問題（問115）へ