大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問8 (数学Ⅰ・数学A(第1問) 問8)
問題文
水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
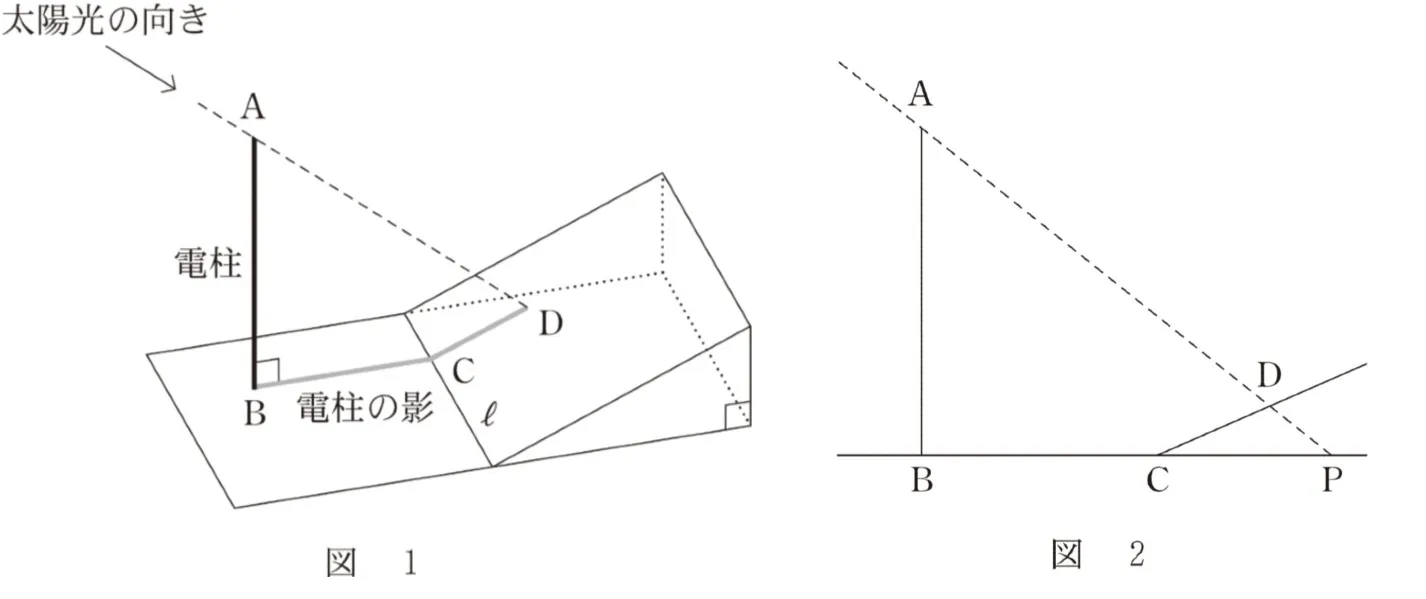
図1のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには7%と表示されているとする。
電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線をlとする。
電柱の先端を点Aとし、根もとを点Bとする。電柱の影について、地面にある部分を線分BCとし、坂にある部分を線分CDとする。線分BC、CDがそれぞれlと垂直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
電柱の影が坂に向かってまっすぐにのびているとする。このとき、4点A、B、C、Dを通る平面はlと垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは∠APBの大きさのことである。
道路標識の7%という表示は、この坂をのぼったとき、100mの水平距離に対して7mの割合で高くなることを示している。nを1以上9以下の整数とするとき、坂の傾斜角∠DCPの大きさについて
n°<∠DCP<n°+1°
を満たすnの値は( シ )である。
以下では、∠DCPの大きさは、ちょうど( シ )°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC=7m、CD=4mであり、太陽高度は∠APB=45°であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき
BE=( ス )✕( セ )m
であり
DE=([ ソ ]+[ タ ]✕[ チ ])m
である。よって、電柱の高さは、小数第2位で四捨五入すると( ツ )mであることがわかる。
( ソ )、( タ )、( チ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問8(数学Ⅰ・数学A(第1問) 問8) (訂正依頼・報告はこちら)
水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
図1のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには7%と表示されているとする。
電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線をlとする。
電柱の先端を点Aとし、根もとを点Bとする。電柱の影について、地面にある部分を線分BCとし、坂にある部分を線分CDとする。線分BC、CDがそれぞれlと垂直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
電柱の影が坂に向かってまっすぐにのびているとする。このとき、4点A、B、C、Dを通る平面はlと垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは∠APBの大きさのことである。
道路標識の7%という表示は、この坂をのぼったとき、100mの水平距離に対して7mの割合で高くなることを示している。nを1以上9以下の整数とするとき、坂の傾斜角∠DCPの大きさについて
n°<∠DCP<n°+1°
を満たすnの値は( シ )である。
以下では、∠DCPの大きさは、ちょうど( シ )°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC=7m、CD=4mであり、太陽高度は∠APB=45°であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき
BE=( ス )✕( セ )m
であり
DE=([ ソ ]+[ タ ]✕[ チ ])m
である。よって、電柱の高さは、小数第2位で四捨五入すると( ツ )mであることがわかる。
( ソ )、( タ )、( チ )にあてはまるものを1つ選べ。

- ソ:5 タ:3 チ:sin∠DCP
- ソ:6 タ:2 チ:1/sin∠DCP
- ソ:6 タ:3 チ:1/cos∠DCP
- ソ:7 タ:4 チ:cos∠DCP
- ソ:7 タ:5 チ:tan∠DCP
- ソ:8 タ:5 チ:1/tan∠DCP
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
三角比の性質から、
DE=BC+CDcos∠DCP
となりますので、
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
となります。
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より誤
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より誤
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より誤
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より正
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より誤
ソに入るのは7
タに入るのは4
チに入るのはcos∠DCP
より誤
三角比の基本的な性質は至る所で使います。
特に、直角三角形の斜辺の長さaと直角以外の角Θが1つ与えられているとき、
ほかの2つの長さをa,Θのみを用いて表す方法は頻出です。
ぜひ押さえておきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問7)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問9)へ