大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
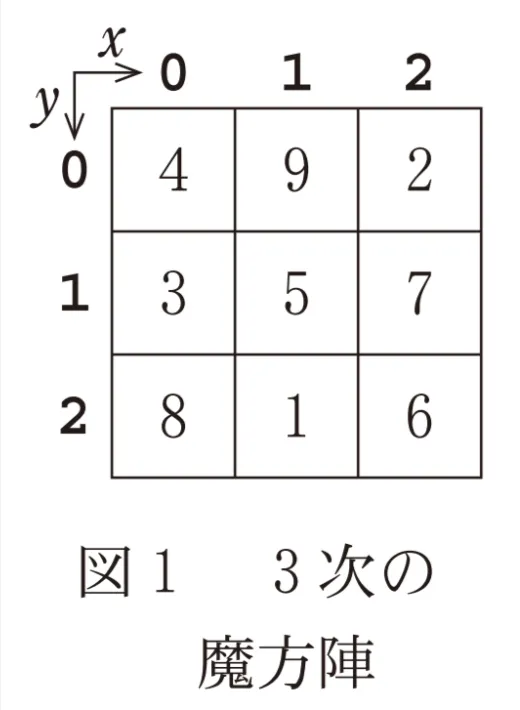
問159 (情報関係基礎(第3問) 問12)
問題文
● まず、図5(a)に示すように、一番下の行の中央に1を記入する。
● 2以降の数zについては、基本的に、その前にz−1を記入したマスの右下のマスに記入する。
○ ただし、右下のマスが表の外側になるとき、下にはみ出る場合は一番上の行に、右にはみ出る場合は一番左の列に回り込む。右にも下にもはみ出る場合は、第0列第0行に回り込む。
○ 記入しようとするマスにすでに数が記入されていた場合は、z−1を記入したマスの一つ上のマスに記入する。
この手順を用いて3次の魔方陣を作成する。2を記入するときに下にはみ出るので、一番上の行に回り込む(図5(b))。これは9を記入するときも同様である。また、3を記入するときに右にはみ出るので、一番左の列に回り込む(図5(c))。これは8を記入するときも同様である。さらに、4を記入するときに3の右下のマスが埋まっているので、3の上のマスに記入する(図5(d))。なお、7を記入するとき、6の右下のマスは、右にも下にもはみ出るので、第0列第0行に回り込むが、すでに4が記入されているので、6がある第2列第2行の上のマスに記入する。完成形が図5(e)である。
この作成方法を手続きとしたものが図6である。配列Mahouに、作成する魔方陣のマスの値を格納していく。Mahou[x,y]の値が0のときは、そのマスは未記入であることを表している。最初に記入するマスの場所をNを用いて表すと、第( カ )列、第( キ )行となり、(03)行目で格納している。なお、a%bは、aをbで割った余りを求める演算である。
この手続きを実行すると、(06)行目は( ク )回実行される。
図6 3次の魔法陣を作成する手続き
(01)配列Mahouのすべての要素に0を代入する
(02)N←3
(03)x←( カ ),y←( キ ),Mahou[x,y]←1
(04)zを2からN✕Nまで1ずつ増やしながら,
(05)│ もしMahou[(x+1)%N,(y+1)%N]=0ならば
(06)│ │ x←( ケ ),y←( コ )
(07)│ を実行し,そうでなければ
(08)│ │( サ )
(09)│ を実行する
(10)│ Mahou[x,y]←z
(11)を繰り返す
(2)の手順に従って、Nの値が3より大きい魔方陣を作成した。これが正しい魔方陣になっていることを検証したい。そのために作成した手続きの一部が、図7・図8である。問1では各列や各行、各対角方向の和を表示するのみであったが、ここではそれらが同一であることを手続き内で検証する。図7では、変数hantei_waと変数batuを用いて配列Mahouの各行の和が一致することを検証する。hantei_waには最初の行の和を格納し、以降の行の和がこれと一致しない場合はbatuの値を1とする。最終的にbatuの値に応じてメッセージを表示する。なお、各列の和や対角方向の和についても同様に検証できる。
図8は、配列Mahouに1からN✕Nまでのすべての数が重複なく入っていることを検証する手続きである。ここでは、1次元配列Kakuninを用いている。また、図7と同じ用途で変数batuを用いている。
図7 各行の和が一致することの検証
(01)hantei_wa←0,batu←0
(02)gyouを0からN−1まで1ずつ増やしながら,
(03)│ wa←0
(04)│ retuを0からN−1まで1ずつ増やしながら,
(05)│ │ wa←wa+( ウ )
(06)│ を繰り返す
(07)│ もし( シ )ならばhantei_wa←waを実行する
(08)│( ス )
(09)│ を繰り返す
(10)もしbatu=1ならば「魔法陣ではありません!」を表示し,
そうでなければ「各行の和は一致しました」を表示する
図8 すべての数が重複なく入っていることの検証
(01)配列kakuninのすべての要素に0を代入する
(02)batu←0
(03)gyouを0からN−1まで1ずつ増やしながら,
(04)│ retuを0からN−1まで1ずつ増やしながら,
(05)│ │ Kakunin[( セ )]を1増やす
(06)│ を繰り返す
(07)を繰り返す
(08)iを1からN✕Nまで1ずつ増やしながら,
(09)│ もし( ソ )ならばbatu←( タ )を実行する
(10)を繰り返す
(11)もしbatu=1ならば「魔法陣ではありません!」を表示し,
そうでなければ「数の重複はありませんでした」を表示する
( シ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問159(情報関係基礎(第3問) 問12) (訂正依頼・報告はこちら)
● まず、図5(a)に示すように、一番下の行の中央に1を記入する。
● 2以降の数zについては、基本的に、その前にz−1を記入したマスの右下のマスに記入する。
○ ただし、右下のマスが表の外側になるとき、下にはみ出る場合は一番上の行に、右にはみ出る場合は一番左の列に回り込む。右にも下にもはみ出る場合は、第0列第0行に回り込む。
○ 記入しようとするマスにすでに数が記入されていた場合は、z−1を記入したマスの一つ上のマスに記入する。
この手順を用いて3次の魔方陣を作成する。2を記入するときに下にはみ出るので、一番上の行に回り込む(図5(b))。これは9を記入するときも同様である。また、3を記入するときに右にはみ出るので、一番左の列に回り込む(図5(c))。これは8を記入するときも同様である。さらに、4を記入するときに3の右下のマスが埋まっているので、3の上のマスに記入する(図5(d))。なお、7を記入するとき、6の右下のマスは、右にも下にもはみ出るので、第0列第0行に回り込むが、すでに4が記入されているので、6がある第2列第2行の上のマスに記入する。完成形が図5(e)である。
この作成方法を手続きとしたものが図6である。配列Mahouに、作成する魔方陣のマスの値を格納していく。Mahou[x,y]の値が0のときは、そのマスは未記入であることを表している。最初に記入するマスの場所をNを用いて表すと、第( カ )列、第( キ )行となり、(03)行目で格納している。なお、a%bは、aをbで割った余りを求める演算である。
この手続きを実行すると、(06)行目は( ク )回実行される。
図6 3次の魔法陣を作成する手続き
(01)配列Mahouのすべての要素に0を代入する
(02)N←3
(03)x←( カ ),y←( キ ),Mahou[x,y]←1
(04)zを2からN✕Nまで1ずつ増やしながら,
(05)│ もしMahou[(x+1)%N,(y+1)%N]=0ならば
(06)│ │ x←( ケ ),y←( コ )
(07)│ を実行し,そうでなければ
(08)│ │( サ )
(09)│ を実行する
(10)│ Mahou[x,y]←z
(11)を繰り返す
(2)の手順に従って、Nの値が3より大きい魔方陣を作成した。これが正しい魔方陣になっていることを検証したい。そのために作成した手続きの一部が、図7・図8である。問1では各列や各行、各対角方向の和を表示するのみであったが、ここではそれらが同一であることを手続き内で検証する。図7では、変数hantei_waと変数batuを用いて配列Mahouの各行の和が一致することを検証する。hantei_waには最初の行の和を格納し、以降の行の和がこれと一致しない場合はbatuの値を1とする。最終的にbatuの値に応じてメッセージを表示する。なお、各列の和や対角方向の和についても同様に検証できる。
図8は、配列Mahouに1からN✕Nまでのすべての数が重複なく入っていることを検証する手続きである。ここでは、1次元配列Kakuninを用いている。また、図7と同じ用途で変数batuを用いている。
図7 各行の和が一致することの検証
(01)hantei_wa←0,batu←0
(02)gyouを0からN−1まで1ずつ増やしながら,
(03)│ wa←0
(04)│ retuを0からN−1まで1ずつ増やしながら,
(05)│ │ wa←wa+( ウ )
(06)│ を繰り返す
(07)│ もし( シ )ならばhantei_wa←waを実行する
(08)│( ス )
(09)│ を繰り返す
(10)もしbatu=1ならば「魔法陣ではありません!」を表示し,
そうでなければ「各行の和は一致しました」を表示する
図8 すべての数が重複なく入っていることの検証
(01)配列kakuninのすべての要素に0を代入する
(02)batu←0
(03)gyouを0からN−1まで1ずつ増やしながら,
(04)│ retuを0からN−1まで1ずつ増やしながら,
(05)│ │ Kakunin[( セ )]を1増やす
(06)│ を繰り返す
(07)を繰り返す
(08)iを1からN✕Nまで1ずつ増やしながら,
(09)│ もし( ソ )ならばbatu←( タ )を実行する
(10)を繰り返す
(11)もしbatu=1ならば「魔法陣ではありません!」を表示し,
そうでなければ「数の重複はありませんでした」を表示する
( シ )にあてはまるものを1つ選べ。

- retu=0
- wa=0
- hantei_wa=0
- wa=hantei_wa
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問158)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問160)へ