大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問31 (数学Ⅰ・数学A(第3問) 問5)
問題文
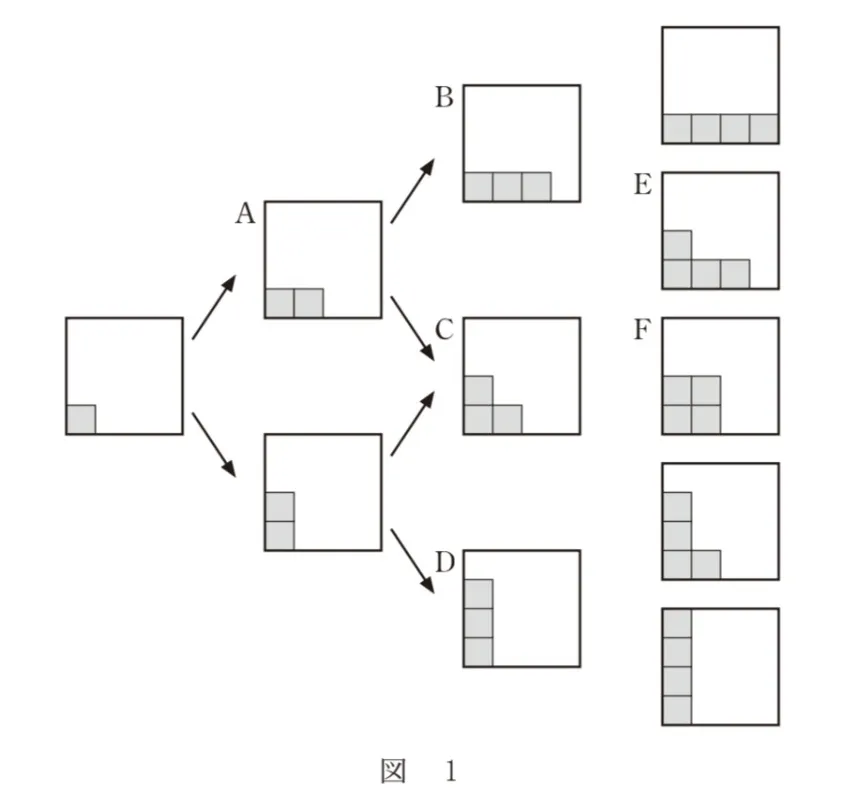
このとき、1枚目のタイルは壁の左下の隅に貼られることになる。また、2枚目のタイルを貼る位置の候補は、1枚目のタイルのすぐ右かすぐ上の2箇所となる。同様に考えると、4枚目のタイルを貼るまでのタイルの配置は、図1のようになる。ただし、図1における矢印はタイルの配置の推移を表している。なお、3枚目から4枚目の間の矢印は省略している。
以下、タイルの配置を、単に配置という。
(3)4枚目のタイルを貼った時点での配置を考える。
(ⅰ)4枚目のタイルを貼った時点での配置が図1のEとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB、C、Dのうち( ケ )である。したがって、4枚目のタイルを貼った時点での配置が図1のEとなる確率は( コ )/( サシ )である。
4枚目のタイルを貼った時点での配置が図1のFとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB、C、Dのうち( ス )である。したがって、4枚目のタイルを貼った時点での配置が図1のFとなる確率は( セ )/( ソ )である。
( コ )、( サシ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問31(数学Ⅰ・数学A(第3問) 問5) (訂正依頼・報告はこちら)
このとき、1枚目のタイルは壁の左下の隅に貼られることになる。また、2枚目のタイルを貼る位置の候補は、1枚目のタイルのすぐ右かすぐ上の2箇所となる。同様に考えると、4枚目のタイルを貼るまでのタイルの配置は、図1のようになる。ただし、図1における矢印はタイルの配置の推移を表している。なお、3枚目から4枚目の間の矢印は省略している。
以下、タイルの配置を、単に配置という。
(3)4枚目のタイルを貼った時点での配置を考える。
(ⅰ)4枚目のタイルを貼った時点での配置が図1のEとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB、C、Dのうち( ケ )である。したがって、4枚目のタイルを貼った時点での配置が図1のEとなる確率は( コ )/( サシ )である。
4枚目のタイルを貼った時点での配置が図1のFとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB、C、Dのうち( ス )である。したがって、4枚目のタイルを貼った時点での配置が図1のFとなる確率は( セ )/( ソ )である。
( コ )、( サシ )にあてはまるものを1つ選べ。

- コ:1 サシ:12
- コ:3 サシ:16
- コ:5 サシ:21
- コ:7 サシ:24
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答 コ:7 サシ:24
解説
Eとなる確率を求める問題です。
以下では、
・○となる確率をP(○)
・△を経由したという条件のもとで☆となる条件付き確率をP△(☆)
・▲を経由してかつ★となる確率をP(▲∩★)
と書くことにします。
また、2枚目を貼った時点でのAでない方をA'と呼ぶことにします。
前問より、ケに当てはまるのは「BとCだけ」でした。
Bを経由するかCを経由するかで場合分けして考えます。
P(B)=P(A)PA(B)=(1/2)✕(1/2)=1/4
P(A∩C)=P(A)PA(C)=(1/2)✕(1/2)=1/4
P(A'∩C)=P(A')PA'(C)=(1/2)✕(1/2)=1/4
P(C)=P(A∩C)+P(A'∩C)=(1/4)+(1/4)=1/2
PB(E)=1/2
PC(E)=1/3
P(B∩E)=P(B)PB(E)=(1/4)・(1/2)=1/8
P(C∩E)=P(C)PC(E)=(1/2)・(1/3)=1/6
P(E)
=P(B∩E)+P(C∩E)
=(1/8)+(1/6)
=(3/24)+(4/24)
=7/24
となります。
よって答えは「コ:7 サシ:24」となります。
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
前の問題(問30)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問32)へ