大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問177 (情報関係基礎(第4問) 問19)
問題文
なお、以下の問題を解答するにあたっては、使用する 表計算ソフトウェアの説明(リンク) を参照するとよい。
Yさんは、かねてより夢であったパンの移動販売をすることになった。
2か所で正式に販売を開始して4週間が経ったが、売れ残りが多く出た。そこで、できるだけパンを残さず、かつ販売途中で品切れにならないように、パンの製造個数を検討することにした。さらに、パンの売れ残りが出ないような販売方法についても検討した。
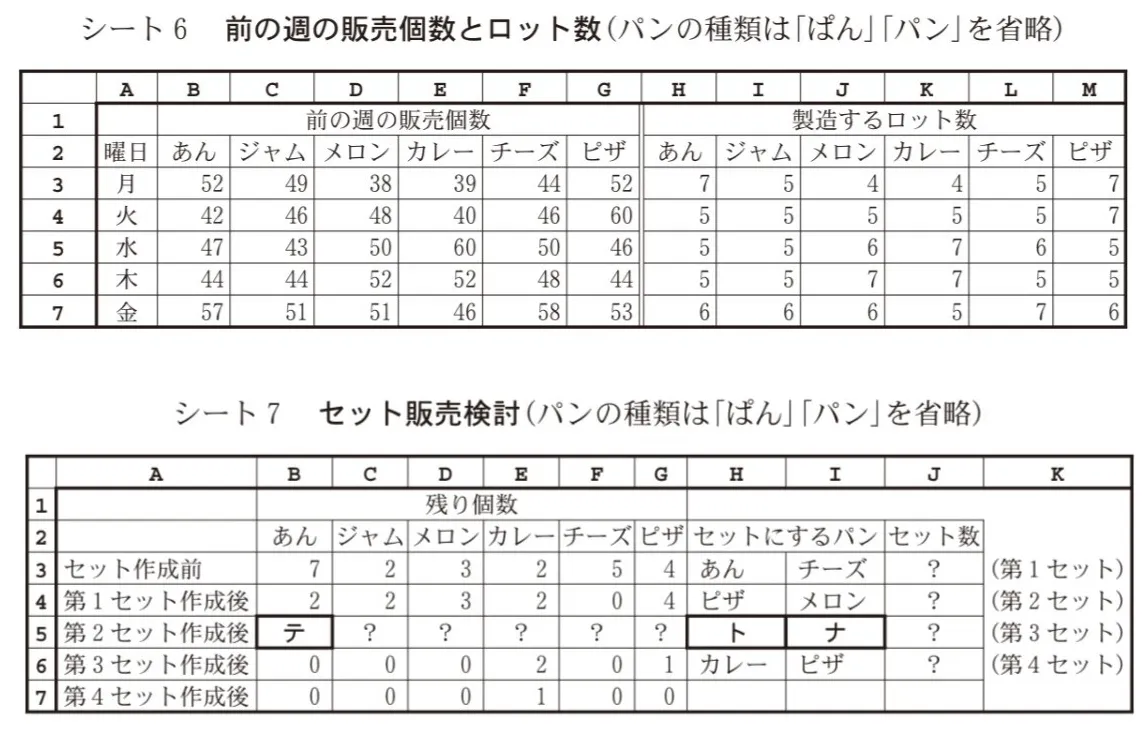
パンの製造は、同じ種類のパン10個を1ロットとし、ロット単位でしか製造できない。製造するロット数は、前の週の同曜日の販売個数をもとにすることにした。適切なロット数を求めるため、シート6前の週の販売個数とロット数を作成した。セル範囲B3~G7には前の週の同曜日の販売個数を入力し、ロット数を次のルールで求めることにした。
・販売個数を10で割り小数点以下を切り上げた整数をロット数とする。
・販売個数が同じ曜日の中で最大、あるいは販売個数が10の倍数の場合にはさらに1ロット増やす。
このルールに従ってロット数を求める次の計算式をセルH3に入力し、セル範囲H4~H7とセル範囲I3~M7に複写した。
( ソ )+IF(OR(B3=[ タ ],[ チ ]=0),1,[ ツ ])
次に、売れ残りが出そうな場合に、異なる種類のパン2個を組み合わせて販売することを考えた。どの組合せが良いかを検討するため、シート7セット販売検討を作成し、パンの組合せを順次求めていくことにした。なお、設問の都合により、値を「?」で隠している箇所がある。
まずは、閉店1時間前における残り個数が多い順に2種類のパンを組み合わせて、できる限り多くのセットを作り、さらに残ったパンの多いものから順に、同様に組み合わせていくという方法を試すことにした。
セル範囲B3~G3には閉店1時間前のパンの残り個数を入力するものとし、動作確認のために仮の値を入力した。列Hと列Iには同じ行の残り個数にもとづいてセットにするパンの種類を二つ、列Jにはそのときに作成できるセットの数(セット数)を求めるための適切な計算式をそれぞれ入力した。なお、残り個数が同じパンがある場合は、シート7のセル範囲B2~G2の中で左にあるパンから優先してセットにすることにした。セットを作成した後に残ったパンの個数を順に求めるため、セルB4に次の計算式を入力し、セル範囲B5~B7とセル範囲C4~G7に複写した。
IF(OR(B$2=[ ニ ],B$2=[ ヌ ]),B3−[ ネ ],B3)
Yさんはシート7の処理を確認した。その結果、第2セット作成後のあんぱんは( テ )個、第3セットでセットにするパンは( ト )と( ナ )になり、他のセルも正しく処理されていることが確認できた。Yさんは、今後もより良いセットの組合せ方法や販売方法などについて検討し続けることになる。
( ニ )、( ヌ )にあてはまるものを2つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問177(情報関係基礎(第4問) 問19) (訂正依頼・報告はこちら)
なお、以下の問題を解答するにあたっては、使用する 表計算ソフトウェアの説明(リンク) を参照するとよい。
Yさんは、かねてより夢であったパンの移動販売をすることになった。
2か所で正式に販売を開始して4週間が経ったが、売れ残りが多く出た。そこで、できるだけパンを残さず、かつ販売途中で品切れにならないように、パンの製造個数を検討することにした。さらに、パンの売れ残りが出ないような販売方法についても検討した。
パンの製造は、同じ種類のパン10個を1ロットとし、ロット単位でしか製造できない。製造するロット数は、前の週の同曜日の販売個数をもとにすることにした。適切なロット数を求めるため、シート6前の週の販売個数とロット数を作成した。セル範囲B3~G7には前の週の同曜日の販売個数を入力し、ロット数を次のルールで求めることにした。
・販売個数を10で割り小数点以下を切り上げた整数をロット数とする。
・販売個数が同じ曜日の中で最大、あるいは販売個数が10の倍数の場合にはさらに1ロット増やす。
このルールに従ってロット数を求める次の計算式をセルH3に入力し、セル範囲H4~H7とセル範囲I3~M7に複写した。
( ソ )+IF(OR(B3=[ タ ],[ チ ]=0),1,[ ツ ])
次に、売れ残りが出そうな場合に、異なる種類のパン2個を組み合わせて販売することを考えた。どの組合せが良いかを検討するため、シート7セット販売検討を作成し、パンの組合せを順次求めていくことにした。なお、設問の都合により、値を「?」で隠している箇所がある。
まずは、閉店1時間前における残り個数が多い順に2種類のパンを組み合わせて、できる限り多くのセットを作り、さらに残ったパンの多いものから順に、同様に組み合わせていくという方法を試すことにした。
セル範囲B3~G3には閉店1時間前のパンの残り個数を入力するものとし、動作確認のために仮の値を入力した。列Hと列Iには同じ行の残り個数にもとづいてセットにするパンの種類を二つ、列Jにはそのときに作成できるセットの数(セット数)を求めるための適切な計算式をそれぞれ入力した。なお、残り個数が同じパンがある場合は、シート7のセル範囲B2~G2の中で左にあるパンから優先してセットにすることにした。セットを作成した後に残ったパンの個数を順に求めるため、セルB4に次の計算式を入力し、セル範囲B5~B7とセル範囲C4~G7に複写した。
IF(OR(B$2=[ ニ ],B$2=[ ヌ ]),B3−[ ネ ],B3)
Yさんはシート7の処理を確認した。その結果、第2セット作成後のあんぱんは( テ )個、第3セットでセットにするパンは( ト )と( ナ )になり、他のセルも正しく処理されていることが確認できた。Yさんは、今後もより良いセットの組合せ方法や販売方法などについて検討し続けることになる。
( ニ )、( ヌ )にあてはまるものを2つ選べ。

- H$3
- $H3
- H$4
- $H4
- I$3
- $I3
- I$4
- $I4
- J$3
- $J3
- J$4
- $J4
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問176)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問178)へ