2級土木施工管理技士 過去問
令和7年度（前期）
問4 (土木（ユニットA） 問4)
問題文
下図において、点Oの周りに矢印の向きで力P1、P2が作用する場合において、点Oに対する力のモーメント（Mo）は次の値のうち、正しいものはどれか。
ただし、各力のモーメントの符号は、点Oを中心として時計まわりを正、反時計まわりを負とする。
ただし、各力のモーメントの符号は、点Oを中心として時計まわりを正、反時計まわりを負とする。
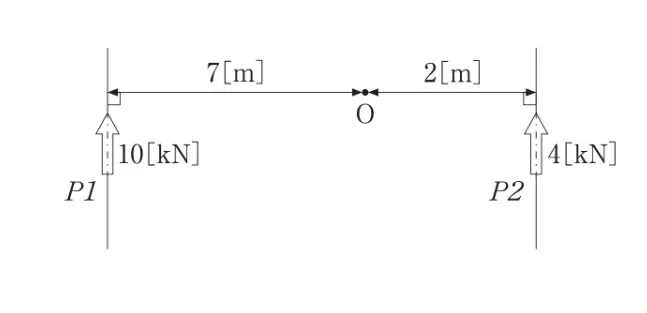
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
2級土木施工管理技士試験 令和7年度（前期） 問4（土木（ユニットA） 問4） （訂正依頼・報告はこちら）
下図において、点Oの周りに矢印の向きで力P1、P2が作用する場合において、点Oに対する力のモーメント（Mo）は次の値のうち、正しいものはどれか。
ただし、各力のモーメントの符号は、点Oを中心として時計まわりを正、反時計まわりを負とする。
ただし、各力のモーメントの符号は、点Oを中心として時計まわりを正、反時計まわりを負とする。
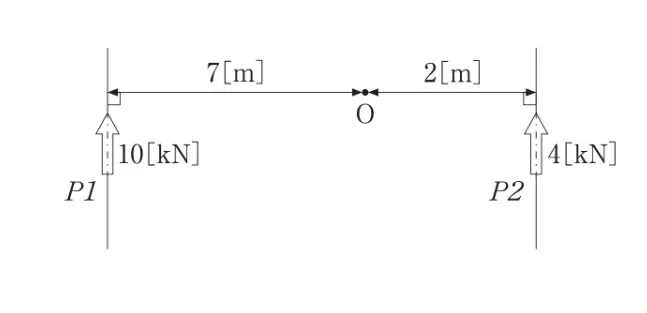
- Mo＝62［kN・m］
- Mo＝44［kN・m］
- Mo＝38［kN・m］
- Mo＝22［kN・m］
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問3）へ
令和7年度（前期） 問題一覧
次の問題（問5）へ