二級建築士過去問
令和6年（2024年）
問52 (学科3（建築構造）問2)

問題文

図のような等分布荷重を受ける幅300mmの矩形断面の単純梁において、A点の最大曲げ応力度が10N／mm²となるときの梁のせいの値として、最も近いものは、次のうちどれか。ただし、部材の断面は一様とし、自重は無視するものとする。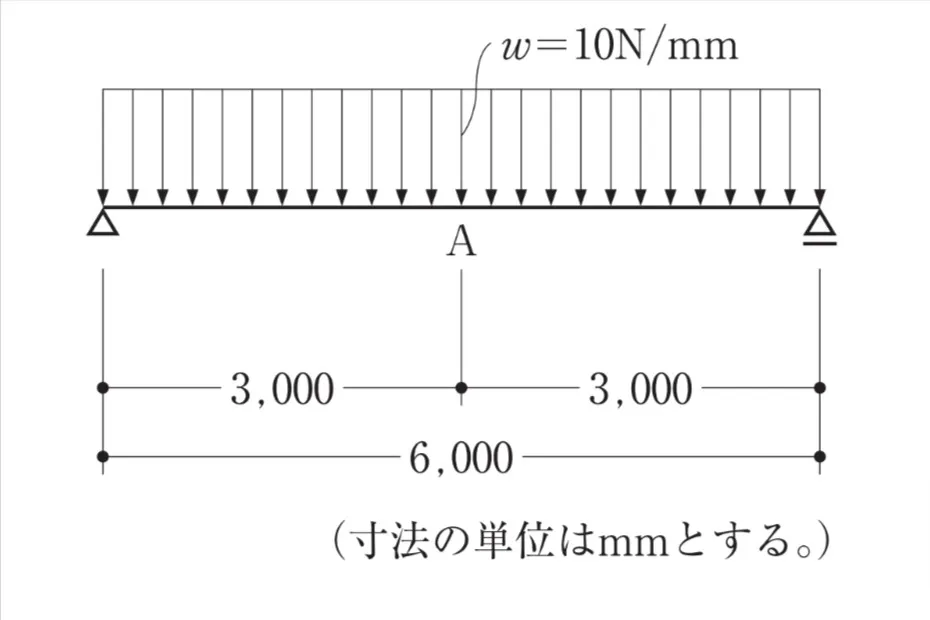問題文の画像

付箋

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

問題

二級建築士試験令和6年（2024年）問52（学科3（建築構造）問2）（訂正依頼・報告はこちら）

図のような等分布荷重を受ける幅300mmの矩形断面の単純梁において、A点の最大曲げ応力度が10N／mm²となるときの梁のせいの値として、最も近いものは、次のうちどれか。ただし、部材の断面は一様とし、自重は無視するものとする。

正解！素晴らしいです

残念...

300 mmが最も近い値になります。

等分布荷重が掛かった幅300 mmの矩形断面において、最大曲げモーメントは
M＝wL²／8＝10 N/mm×6000²mm²／8＝45000000N·mm です。

矩形断面の曲げ応力度は
σ＝6M／(b h²) で表せます。

σ＝10N/mm²、b＝300mm を代入して h を解くと
h＝√{6M／(b σ)}＝√90000＝300mm となります。

選択肢1. 210mm

曲げ応力度は約20N/mm²となり、許容値10N/mm²を大きく上回ります。

断面が小さ過ぎます。

選択肢2. 300mm

計算値と一致し、曲げ応力度がちょうど10N/mm²になります。

適切な断面寸法です。

選択肢3. 420mm

曲げ応力度は約5N/mm²まで下がります。

強度上は安全ですが、材料を余分に使う大きさです。

選択肢4. 600mm

曲げ応力度は約2.5N/mm²となり、必要以上に小さくなります。

過大な断面です。

選択肢5. 840mm

曲げ応力度は約1.3N/mm²まで下がります。

著しく大きく、無駄が多い寸法です。

まとめ

矩形断面の梁では、曲げ応力度 σ＝6M／(b h²) を利用して必要な h を手早く求められます。

今回の条件では300mmが荷重に見合う最小限の大きさで、これより小さいと強度不足、大きいと材料の無駄が生じます。

参考になった数7