大学入学共通テスト（数学） 過去問
令和4年度（2022年度）追・再試験
問22 (数学Ⅰ・数学A（第2問） 問5)
問題文
以下（ ケコ ）・（ サ ）に当てはまる組み合わせとして正しいものを選べ。
aを5＜a＜10を満たす実数とする。長方形ABCDを考え、AB＝CD＝5、BC＝DA＝aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
（1）a＝6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP＜（ ア ）である。
このとき、四角形QRSTの面積の最大値は（ イウ ）／（ エ ）である。
a＝8のとき、四角形QRSTの面積の最大値は（ オカ ）である。
（2）5＜a＜10とする。lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は
0≦AP＜（ キク ）−a ・・・・・①
である。
点Pが①を満たす範囲を動くとする。四角形QRSTの面積の最大値が（ イウ ）／（ エ ）となるときのaの値の範囲は
5＜a≦（ ケコ ）／（ サ ）
である。
aが（ ケコ ）／（ サ ）＜a＜10を満たすとき、Pが①を満たす範囲を動いたときの四角形QRSTの面積の最大値は
（ シス ）a2＋（ セソ ）a−（ タチツ ）
である。
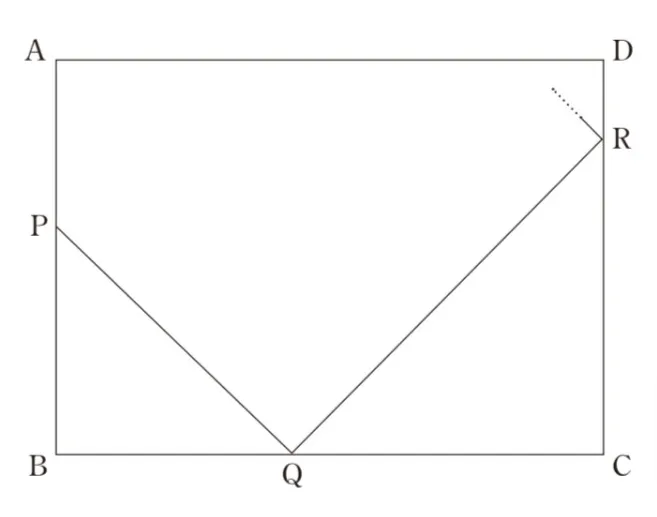
aを5＜a＜10を満たす実数とする。長方形ABCDを考え、AB＝CD＝5、BC＝DA＝aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
（1）a＝6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP＜（ ア ）である。
このとき、四角形QRSTの面積の最大値は（ イウ ）／（ エ ）である。
a＝8のとき、四角形QRSTの面積の最大値は（ オカ ）である。
（2）5＜a＜10とする。lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は
0≦AP＜（ キク ）−a ・・・・・①
である。
点Pが①を満たす範囲を動くとする。四角形QRSTの面積の最大値が（ イウ ）／（ エ ）となるときのaの値の範囲は
5＜a≦（ ケコ ）／（ サ ）
である。
aが（ ケコ ）／（ サ ）＜a＜10を満たすとき、Pが①を満たす範囲を動いたときの四角形QRSTの面積の最大値は
（ シス ）a2＋（ セソ ）a−（ タチツ ）
である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）追・再試験 問22（数学Ⅰ・数学A（第2問） 問5） （訂正依頼・報告はこちら）
以下（ ケコ ）・（ サ ）に当てはまる組み合わせとして正しいものを選べ。
aを5＜a＜10を満たす実数とする。長方形ABCDを考え、AB＝CD＝5、BC＝DA＝aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
（1）a＝6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP＜（ ア ）である。
このとき、四角形QRSTの面積の最大値は（ イウ ）／（ エ ）である。
a＝8のとき、四角形QRSTの面積の最大値は（ オカ ）である。
（2）5＜a＜10とする。lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は
0≦AP＜（ キク ）−a ・・・・・①
である。
点Pが①を満たす範囲を動くとする。四角形QRSTの面積の最大値が（ イウ ）／（ エ ）となるときのaの値の範囲は
5＜a≦（ ケコ ）／（ サ ）
である。
aが（ ケコ ）／（ サ ）＜a＜10を満たすとき、Pが①を満たす範囲を動いたときの四角形QRSTの面積の最大値は
（ シス ）a2＋（ セソ ）a−（ タチツ ）
である。
aを5＜a＜10を満たす実数とする。長方形ABCDを考え、AB＝CD＝5、BC＝DA＝aとする。
次のようにして、長方形ABCDの辺上に4点P、Q、R、Sをとり、内部に点Tをとることを考える。
辺AB上に点Bと異なる点Pをとる。辺BC上に点Qを∠BPQが45°になるようにとる。Qを通り、直線PQと垂直に交わる直線をlとする。lが頂点C、D以外の点で辺CDと交わるとき、lと辺CDの交点をRとする。
点Rを通りlと垂直に交わる直線をmとする。mと辺ADとの交点をSとする。点Sを通りmと垂直に交わる直線をnとする。nと直線PQとの交点をTとする。
（1）a＝6のとき、lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は0≦AP＜（ ア ）である。
このとき、四角形QRSTの面積の最大値は（ イウ ）／（ エ ）である。
a＝8のとき、四角形QRSTの面積の最大値は（ オカ ）である。
（2）5＜a＜10とする。lが頂点C、D以外の点で辺CDと交わるときのAPの値の範囲は
0≦AP＜（ キク ）−a ・・・・・①
である。
点Pが①を満たす範囲を動くとする。四角形QRSTの面積の最大値が（ イウ ）／（ エ ）となるときのaの値の範囲は
5＜a≦（ ケコ ）／（ サ ）
である。
aが（ ケコ ）／（ サ ）＜a＜10を満たすとき、Pが①を満たす範囲を動いたときの四角形QRSTの面積の最大値は
（ シス ）a2＋（ セソ ）a−（ タチツ ）
である。
- ケコ：12 サ：5
- ケコ：13 サ：4
- ケコ：14 サ：3
- ケコ：15 サ：2
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
前の問題より、
QC=a-5+x
RD=10-a-x
となっています。
また、四角形が形成される条件は、
0≦x<10-a
でした。
ここで四角形の面積をもとめます。三平方の定理(1:1:√2)より
QR=√2QC, RS=√2RD
を用います。
四角形の面積をSとおくと、
S=QR×RS=√2QC×√2RD=2QC×RD=2(a-5+x)(10-a-x)
これを展開すると、
S=-2(x2+(2a-15)x+a2-15a+50)
これを平方完成すると、
S=-2{ (x+(2a-15)/2)2-(25/4) }=-2(x+(2a-15)/2)2+(25/2)
となり、
Sは、x=(15-2a)/2のとき、最大値25/2を取ります。
ここで、Sのグラフを考えましょう。
下図のように、頂点のx座標がx≧0の範囲にあれば、最大値は25/2(グラフでは12.5)となります。
頂点のx座標は平方完成より、 (15-2a)/2 です。
0≦ (15-2a)/2
よって、
a<15/2
が求めるaの条件です。
a<15/2より誤りです。
a<15/2より誤りです。
a<15/2より誤りです。
a<15/2より正解です。
頂点がx>0の範囲にあれば、最大値が25/2になることに気づく必要がある問題でした。
そのためにもグラフを考える事がこの問題でも重要です。
参考になった数0
この解説の修正を提案する
前の問題（問21）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問23）へ