大学入学共通テスト(数学) 過去問
令和5年度(2023年度)本試験
問73 (数学Ⅱ・数学B(第2問) 問9)
問題文
f(x)=x2(k−x)
y=f(x)のグラフとx軸との共有点の座標は(0,0)と([ ア ],0)である。
f(x)の導関数f′(x)は
f′(x)=( イウ )x2+( エ )kx
である。
x=( オ )のとき、f(x)は極小値( カ )をとる。
x=( キ )のとき、f(x)は極大値( ク )をとる。
また、0<x<kの範囲においてx=( キ )のときf(x)は最大となることがわかる。
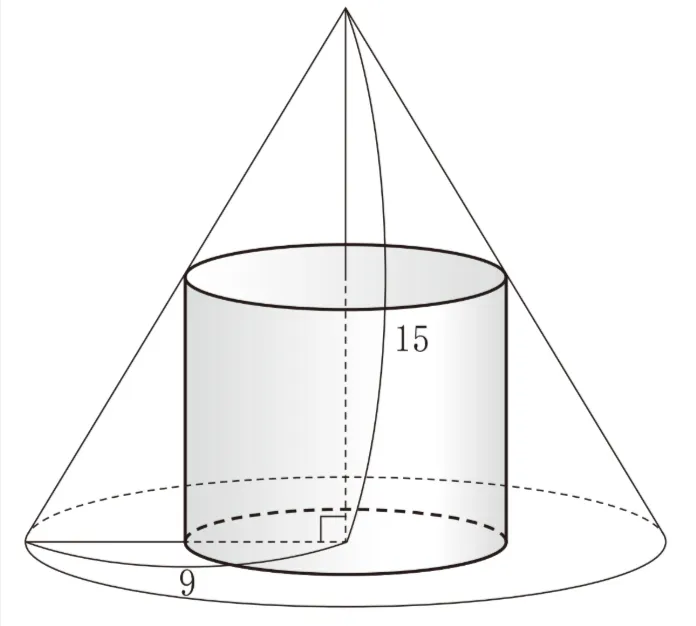
(2)後の図のように底面が半径9の円で高さが15の円錐(すい)に内接する円柱を考える。円柱の底面の半径と体積をそれぞれx、Vとする。Vをxの式で表すと
V=([ ケ ]/[ コ ])πx2([ サ ]−x) (0<x<9)
である。(1)の考察より、x=( シ )のときVは最大となることがわかる。Vの最大値は( スセソ )πである。
( スセソ )にあてはまるものを次のうちから1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和5年度(2023年度)本試験 問73(数学Ⅱ・数学B(第2問) 問9) (訂正依頼・報告はこちら)
f(x)=x2(k−x)
y=f(x)のグラフとx軸との共有点の座標は(0,0)と([ ア ],0)である。
f(x)の導関数f′(x)は
f′(x)=( イウ )x2+( エ )kx
である。
x=( オ )のとき、f(x)は極小値( カ )をとる。
x=( キ )のとき、f(x)は極大値( ク )をとる。
また、0<x<kの範囲においてx=( キ )のときf(x)は最大となることがわかる。
(2)後の図のように底面が半径9の円で高さが15の円錐(すい)に内接する円柱を考える。円柱の底面の半径と体積をそれぞれx、Vとする。Vをxの式で表すと
V=([ ケ ]/[ コ ])πx2([ サ ]−x) (0<x<9)
である。(1)の考察より、x=( シ )のときVは最大となることがわかる。Vの最大値は( スセソ )πである。
( スセソ )にあてはまるものを次のうちから1つ選べ。

- 110
- 140
- 180
- 190
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
最大となるのはx=6のときなので、Vの式
V=(5/3)πx²(9−x)
にx=6を代入します。
V=(5/3)π×6²×(9−6)
=(5/3)π×36×3
=5×36π
=180π
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
この解答は導出の手順・計算結果ともに正しく、論理的に正しいです。
この解答は導出の過程や計算結果に誤りが含まれており、不正解です。
計算ミスのないようにしましょう
参考になった数0
この解説の修正を提案する
前の問題(問72)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問74)へ