大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問20 (数学Ⅰ・数学A(第2問) 問10)
問題文
なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。
(1)太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。
ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、60✕5+30=330(秒)となる。
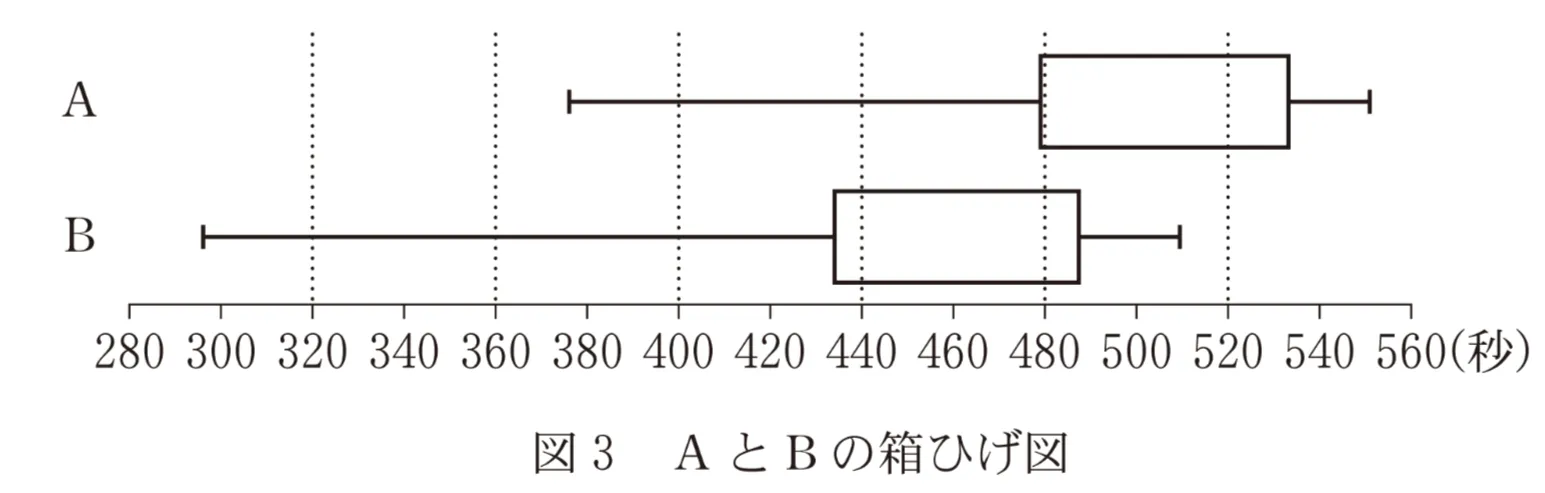
(ⅱ)図3は、A、Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
図3より次のことが読み取れる。ただし、A、Bそれぞれにおける、速い方から13番目の選手は、一人ずつとする。
・Bの速い方から13番目の選手のベストタイムは、Aの速い方から13番目の選手のベストタイムより、およそ( ス )秒速い。
・Aの四分位範囲からBの四分位範囲を引いた差の絶対値は( セ )である。
( セ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問20(数学Ⅰ・数学A(第2問) 問10) (訂正依頼・報告はこちら)
なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。
(1)太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。
ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、60✕5+30=330(秒)となる。
(ⅱ)図3は、A、Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
図3より次のことが読み取れる。ただし、A、Bそれぞれにおける、速い方から13番目の選手は、一人ずつとする。
・Bの速い方から13番目の選手のベストタイムは、Aの速い方から13番目の選手のベストタイムより、およそ( ス )秒速い。
・Aの四分位範囲からBの四分位範囲を引いた差の絶対値は( セ )である。
( セ )にあてはまるものを1つ選べ。

- 0以上20未満
- 20以上40未満
- 40以上60未満
- 60以上80未満
- 80以上100未満
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
「四分位範囲」が何を表すかを考えます。
四分位範囲は、第3四分位数から第1四分位数を引いた値です。
これは箱ひげ図の「箱」の横の長さに相当します。
データAの四分位範囲
第1四分位数=480
第3四分位数≒530
Aの四分位範囲≒530−480≒50
第1四分位数≒435
第3四分位数≒485
Bの四分位範囲≒485-435≒50
|Bの四分位範囲-Aの四分位範囲|≒0
選択肢から適切なものを選択します。
参考になった数0
この解説の修正を提案する
前の問題(問19)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問21)へ