大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問23 (数学Ⅰ・数学A(第2問) 問13)
問題文
なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。
(1)太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。
ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、60✕5+30=330(秒)となる。
(ⅰ)図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
図1からAの最頻値は階級( サ )の階級値である。また、図2からBの中央値が含まれる階級は( シ )である。
(ⅱ)図3は、A、Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
図3より次のことが読み取れる。ただし、A、Bそれぞれにおける、速い方から13番目の選手は、一人ずつとする。
(ⅲ)太郎さんは、Aのある選手とBのある選手のベストタイムの比較において、その二人の選手のベストタイムが速いか遅いかとは別の観点でも考えるために、次の式を満たすzの値を用いて判断することにした。
<式>
(あるデータのある選手のベストタイム)=(そのデータの平均値)+z✕(そのデータの標準偏差)
二人の選手それぞれのベストタイムに対するzの値を比較し、その値の小さい選手の方が優れていると判断する。
表1は、A、Bそれぞれにおける、速い方から1番目の選手(以下、1位の選手)のベストタイムと、データの平均値と標準偏差をまとめたものである。
式と表1を用いると、Bの1位の選手のベストタイムに対するzの値は
z=−( ソ ).( タチ )
である。このことから、Bの1位の選手のベストタイムは、平均値より標準偏差のおよそ( ソ ).( タチ )倍だけ小さいことがわかる。
A、Bそれぞれにおける、1位の選手についての記述として、正しいものは( ツ )である。
(2)太郎さんは、マラソン、10000m、5000mのベストタイムに関連がないかを調べることにした。そのために、2022年末時点でのこれら3種目のベストタイムをすべて確認できた日本人男子選手のうち、マラソンのベストタイムが速い方から50人を選んだ。
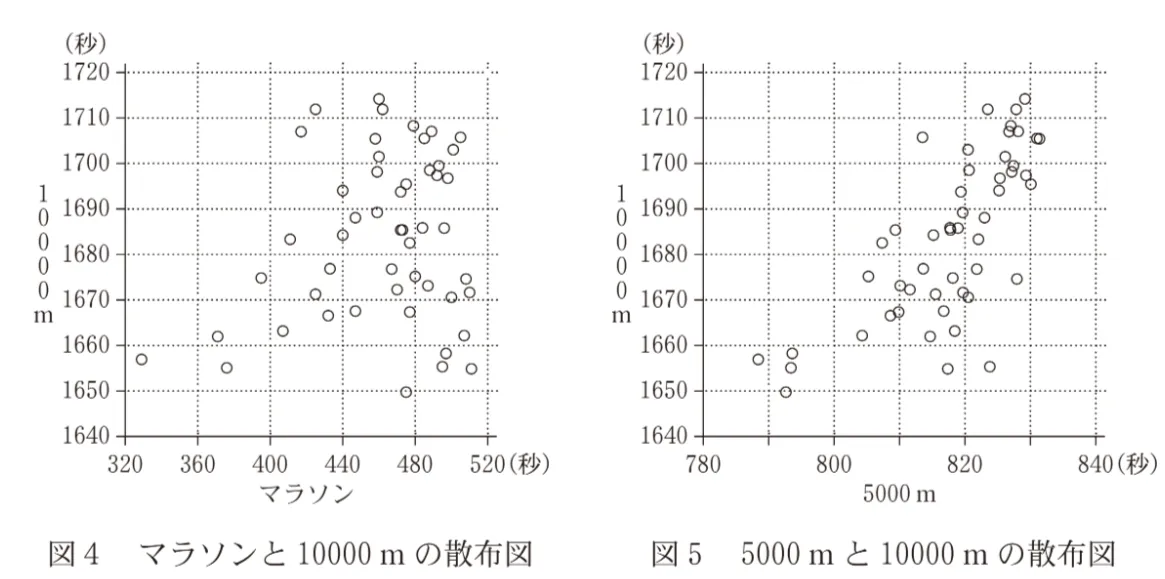
図4と図5はそれぞれ、選んだ50人についてのマラソンと10000mのベストタイム、5000mと10000mのベストタイムの散布図である。ただし、5000mと10000mのベストタイムは秒単位で表し、マラソンのベストタイムは(1)の場合と同様、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。なお、これらの散布図には、完全に重なっている点はない。
次の(a)、(b)は、図4と図5に関する記述である。
(a)マラソンのベストタイムの速い方から3番目までの選手の10000mのベストタイムは、3選手とも1670秒未満である。
(b)マラソンと10000mの間の相関は、5000mと10000mの間の相関より強い。
(a)、(b)の正誤の組合せとして正しいものは( テ )である。
( テ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問23(数学Ⅰ・数学A(第2問) 問13) (訂正依頼・報告はこちら)
なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。
(1)太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。
ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、60✕5+30=330(秒)となる。
(ⅰ)図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
図1からAの最頻値は階級( サ )の階級値である。また、図2からBの中央値が含まれる階級は( シ )である。
(ⅱ)図3は、A、Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
図3より次のことが読み取れる。ただし、A、Bそれぞれにおける、速い方から13番目の選手は、一人ずつとする。
(ⅲ)太郎さんは、Aのある選手とBのある選手のベストタイムの比較において、その二人の選手のベストタイムが速いか遅いかとは別の観点でも考えるために、次の式を満たすzの値を用いて判断することにした。
<式>
(あるデータのある選手のベストタイム)=(そのデータの平均値)+z✕(そのデータの標準偏差)
二人の選手それぞれのベストタイムに対するzの値を比較し、その値の小さい選手の方が優れていると判断する。
表1は、A、Bそれぞれにおける、速い方から1番目の選手(以下、1位の選手)のベストタイムと、データの平均値と標準偏差をまとめたものである。
式と表1を用いると、Bの1位の選手のベストタイムに対するzの値は
z=−( ソ ).( タチ )
である。このことから、Bの1位の選手のベストタイムは、平均値より標準偏差のおよそ( ソ ).( タチ )倍だけ小さいことがわかる。
A、Bそれぞれにおける、1位の選手についての記述として、正しいものは( ツ )である。
(2)太郎さんは、マラソン、10000m、5000mのベストタイムに関連がないかを調べることにした。そのために、2022年末時点でのこれら3種目のベストタイムをすべて確認できた日本人男子選手のうち、マラソンのベストタイムが速い方から50人を選んだ。
図4と図5はそれぞれ、選んだ50人についてのマラソンと10000mのベストタイム、5000mと10000mのベストタイムの散布図である。ただし、5000mと10000mのベストタイムは秒単位で表し、マラソンのベストタイムは(1)の場合と同様、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。なお、これらの散布図には、完全に重なっている点はない。
次の(a)、(b)は、図4と図5に関する記述である。
(a)マラソンのベストタイムの速い方から3番目までの選手の10000mのベストタイムは、3選手とも1670秒未満である。
(b)マラソンと10000mの間の相関は、5000mと10000mの間の相関より強い。
(a)、(b)の正誤の組合せとして正しいものは( テ )である。
( テ )にあてはまるものを1つ選べ。

- (a)正 (b)正
- (a)正 (b)誤
- (a)誤 (b)正
- (a)誤 (b)誤
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
記述(a)の正誤を判断します。
図4の散布図ではタイムが速いほど、値は小さくなるので、グラフの左側に位置する選手ほどマラソンが速いことになります。
縦軸が10000mのベストタイムです。
グラフの最も左側にある点から3つを探し、それぞれの縦軸(10000mのタイム)の値を確認します。
1番速い選手:横軸が340秒付近の点で、縦軸は1650秒台です。
2番目に速い選手:横軸が360秒弱の点で、縦軸は1660秒付近です。
3番目に速い選手:横軸が360秒強の点で、縦軸は1650秒台です。
これらの3つの点は、いずれも縦軸の1670秒の線よりも下にあります。したがって、3選手とも10000mのベストタイムは1670秒未満であると言えます。
よって、記述(a)は正しいです。
記述(b)の正誤を判断します。
相関の強さは、散布図の点がどれだけ直線に近い形で分布しているかで判断できます。
点が直線状に密集しているほど、相関は強いと言えます。
図4: 全体として右上がりの傾向(正の相関)が見られますが、点の散らばりは比較的大きく、ばらつきがあります。
図5: 図4に比べて、点はより明確に右上がりの直線状に集まっており、散らばりが小さいです。
比較すると、図5の方が相関が強いことがわかります。
つまり、「5000mと10000mの間の相関」の方が「マラソンと10000mの間の相関」よりも強いと言えます。
記述(b)はこれとは逆のことを述べているため、(b)は誤りです。
参考になった数0
この解説の修正を提案する
前の問題(問22)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問24)へ