大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問147 (情報関係基礎(第2問) 問17)
問題文
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A~Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
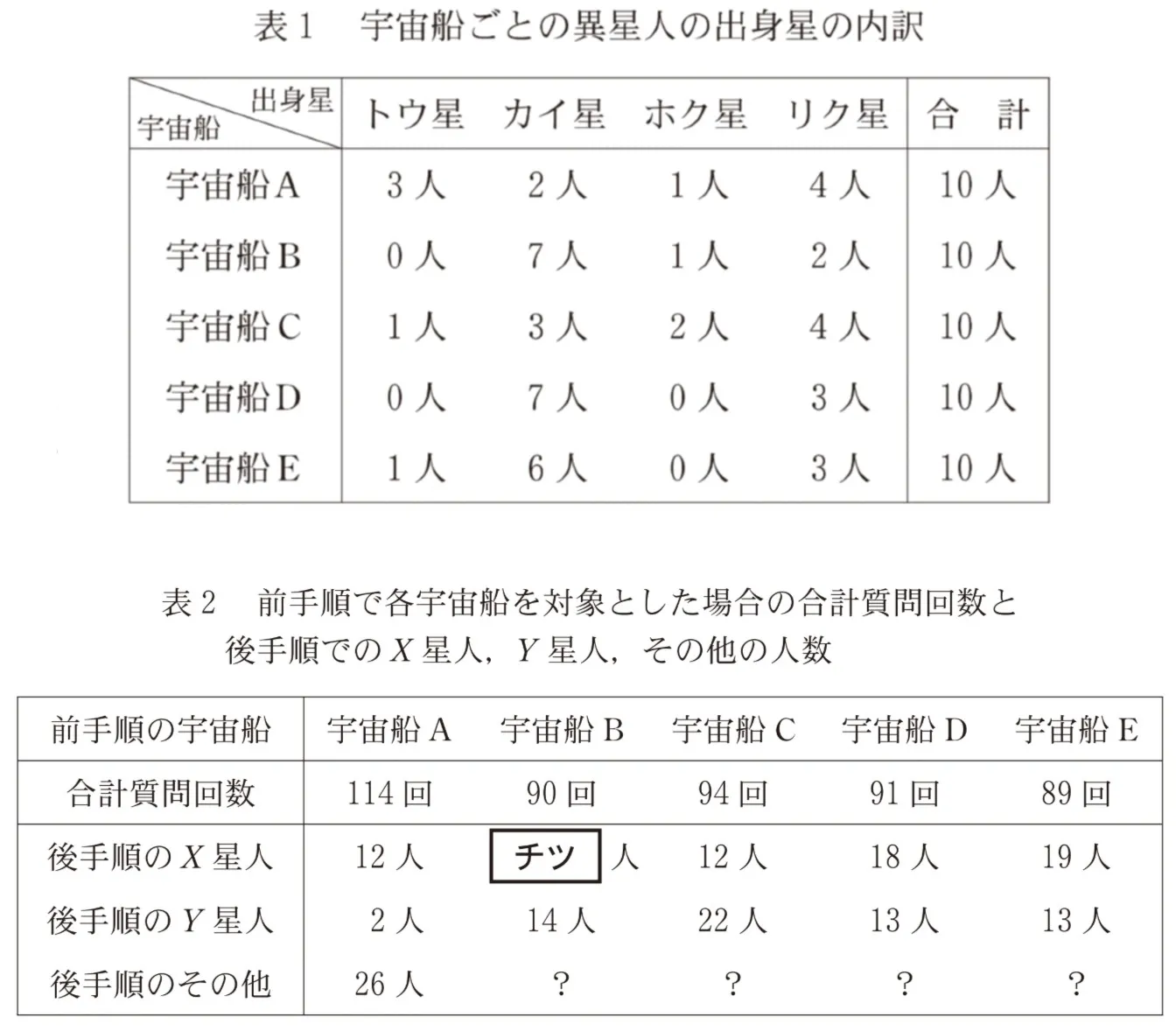
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
Mさんは、まずグループ法で一部の人に出身星をたずね、その結果にもとづいて順次法で残りの人に出身星をたずねることで質問回数が減るという仮説を立て、次の二段法を考えた。
<二段法>
前手順:ある1隻の宇宙船の人にグループ法で出身星をたずね、出身者が最も多い星をX星、2番目をY星として、後手順に進む。
後手順:残りの4隻の人に、順次法で出身星をたずねる。ここでの最初の質問は「X星人ですか?」、次は「Y星人ですか?」とする。
Mさんは、表1のデータを使って二段法をシミュレーションしてみることにした。
例えば、前手順で宇宙船Bを対象としたら、X星はカイ星、Y星はリク星となり、これをふまえて後手順で宇宙船AとC~Eの40人に質問する。一方、前手順でAを対象としたら、X星は( ソ )、Y星は( タ )となる。
Mさんは、前手順で各宇宙船を対象とした場合の合計質問回数を次の表2のとおりに記述し、これらの結果の理由を分析した。分析にあたり、後手順でのX星人、Y星人、その他(X星人でもY星人でもない人)の人数も調べた。なお、設問の都合により、表2の一部を「?」で隠している。
表2では前手順で宇宙船Aを対象とした場合に合計質問回数が多く、宇宙船B・D・Eで少ない。これらの差は、B・D・Eで( テ )ことによる。AとCを比べても合計質問回数に差があるが、これはCの( ト )ことによる。Cでも( テ )わけではないのにCの( ト )のは、( ナ )ためである。また、BとEの合計質問回数の差は、Eの方が( ニ )ことによる。
( ニ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問147(情報関係基礎(第2問) 問17) (訂正依頼・報告はこちら)
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A~Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
Mさんは、まずグループ法で一部の人に出身星をたずね、その結果にもとづいて順次法で残りの人に出身星をたずねることで質問回数が減るという仮説を立て、次の二段法を考えた。
<二段法>
前手順:ある1隻の宇宙船の人にグループ法で出身星をたずね、出身者が最も多い星をX星、2番目をY星として、後手順に進む。
後手順:残りの4隻の人に、順次法で出身星をたずねる。ここでの最初の質問は「X星人ですか?」、次は「Y星人ですか?」とする。
Mさんは、表1のデータを使って二段法をシミュレーションしてみることにした。
例えば、前手順で宇宙船Bを対象としたら、X星はカイ星、Y星はリク星となり、これをふまえて後手順で宇宙船AとC~Eの40人に質問する。一方、前手順でAを対象としたら、X星は( ソ )、Y星は( タ )となる。
Mさんは、前手順で各宇宙船を対象とした場合の合計質問回数を次の表2のとおりに記述し、これらの結果の理由を分析した。分析にあたり、後手順でのX星人、Y星人、その他(X星人でもY星人でもない人)の人数も調べた。なお、設問の都合により、表2の一部を「?」で隠している。
表2では前手順で宇宙船Aを対象とした場合に合計質問回数が多く、宇宙船B・D・Eで少ない。これらの差は、B・D・Eで( テ )ことによる。AとCを比べても合計質問回数に差があるが、これはCの( ト )ことによる。Cでも( テ )わけではないのにCの( ト )のは、( ナ )ためである。また、BとEの合計質問回数の差は、Eの方が( ニ )ことによる。
( ニ )にあてはまるものを1つ選べ。

- 前手順でX星人が多かった
- 前手順でX星人が少なかった
- 前手順でその他が多かった
- 前手順でその他が少なかった
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問146)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問148)へ