大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問50 (数学Ⅰ・数学A(第5問) 問5)
問題文
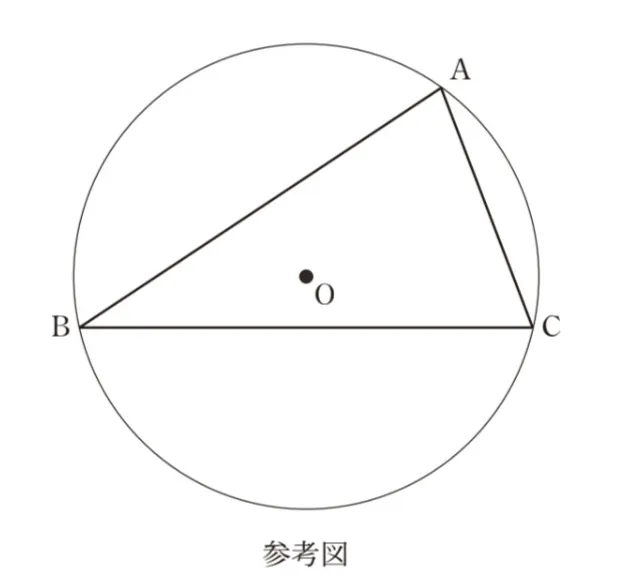
ΔABCの外心をO、垂心をH、内心をIとする。点Oに関して、点A、B、Cと対称な点を、それぞれP、Q、Rとする。直線AHと直線BCとの交点をD、直線BHと直線ACとの交点をEとする。
(2)ΔABCを三つの辺の長さがすべて異なる鋭角三角形とする。このとき、ΔABPと( ク )は相似である。なぜならば、ΔABPと( ク )はいずれも直角三角形であり、また、∠APB=( ケ )が成り立つからである。
このことから、外心O、垂心H、内心Iについての次の命題(a)、(b)の真偽の組合せとして正しいものは( コ )であることがわかる。
(a)直線AOと直線AHは直線AIに関して対称である。
(b)外心Oと垂心Hは直線AIに関して対称である。
( ク )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問50(数学Ⅰ・数学A(第5問) 問5) (訂正依頼・報告はこちら)
ΔABCの外心をO、垂心をH、内心をIとする。点Oに関して、点A、B、Cと対称な点を、それぞれP、Q、Rとする。直線AHと直線BCとの交点をD、直線BHと直線ACとの交点をEとする。
(2)ΔABCを三つの辺の長さがすべて異なる鋭角三角形とする。このとき、ΔABPと( ク )は相似である。なぜならば、ΔABPと( ク )はいずれも直角三角形であり、また、∠APB=( ケ )が成り立つからである。
このことから、外心O、垂心H、内心Iについての次の命題(a)、(b)の真偽の組合せとして正しいものは( コ )であることがわかる。
(a)直線AOと直線AHは直線AIに関して対称である。
(b)外心Oと垂心Hは直線AIに関して対称である。
( ク )にあてはまるものを1つ選べ。

- ΔACP
- ΔADC
- ΔBPC
- ΔPHC
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答 ク:ΔADC
解説
直角三角形ΔABPと相似な三角形を探します。
選択肢はΔACP・ΔADC・ΔBPC・ΔPHCの4つです。
このうち直角三角形なのはΔACPとΔADCの2つです。
円周角の定理より、
∠APB=∠ACB=∠ACD (←これがケの答えとなる)
が成り立つので、適するのはΔADCの方です。
つまり、
・∠ABP=∠ADC=90°
・∠APB=∠ACD
となっていて、ΔABPとΔADCは相似です。
よって答えは「ク:ΔADC」となります。
この選択肢が答えとなります。
参考になった数0
この解説の修正を提案する
前の問題(問49)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問51)へ