大学入学共通テスト（数学） 過去問
令和4年度（2022年度）追・再試験
問100 (数学Ⅱ・数学B（第3問） 問9)
問題文
以下（ ネ ）にあてはまるものを選べ。
問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんのクラスでは、確率分布の問題として、2個のさいころを同時に投げることを72回繰り返す試行を行い、2個とも1の目が出た回数を表す確率変数Xの分布を考えることとなった。そこで、21名の生徒がこの試行を行った。
問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
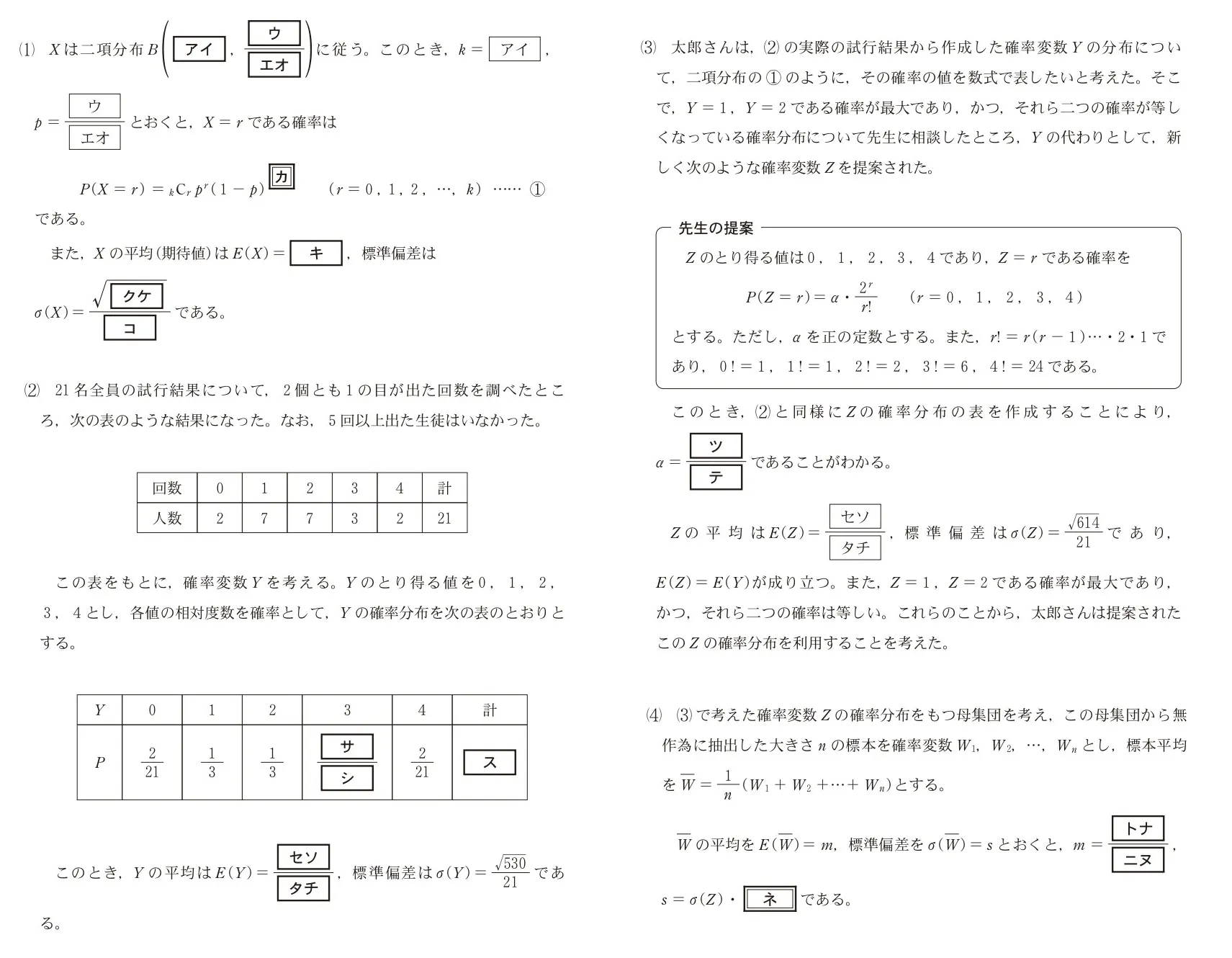
太郎さんのクラスでは、確率分布の問題として、2個のさいころを同時に投げることを72回繰り返す試行を行い、2個とも1の目が出た回数を表す確率変数Xの分布を考えることとなった。そこで、21名の生徒がこの試行を行った。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和4年度（2022年度）追・再試験 問100（数学Ⅱ・数学B（第3問） 問9） （訂正依頼・報告はこちら）
以下（ ネ ）にあてはまるものを選べ。
問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんのクラスでは、確率分布の問題として、2個のさいころを同時に投げることを72回繰り返す試行を行い、2個とも1の目が出た回数を表す確率変数Xの分布を考えることとなった。そこで、21名の生徒がこの試行を行った。
問題を解答するにあたっては、必要に応じて 正規分布表（リンク） を用いてもよい。
太郎さんのクラスでは、確率分布の問題として、2個のさいころを同時に投げることを72回繰り返す試行を行い、2個とも1の目が出た回数を表す確率変数Xの分布を考えることとなった。そこで、21名の生徒がこの試行を行った。
- 1／n
- 1
- 1／√n
- √n
- n
- n2
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
前問同様
母集団（母平均E(Z)、母標準偏差σ(Z)）から大きさnのサンプルを無作為抽出するとき、標本平均Āについて以下が成り立ちます。
期待値(平均)：E(Ā)=E(Z)
分散：V(Ā)=σ(Z)2/n
標準偏差：σ(Ā)=σ(Z)/√n
だから
s=σ(Z)/√n
s=σ(Z)/√nであるため、不正解です。
s=σ(Z)/√nであるため、不正解です。
s=σ(Z)/√nであるため、正解です。
s=σ(Z)/√nであるため、不正解です。
s=σ(Z)/√nであるため、不正解です。
s=σ(Z)/√nであるため、不正解です。
分散の平方根を取ればいいので、標準偏差まで暗記する必要はないです。
参考になった数0
この解説の修正を提案する
前の問題（問99）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問101）へ