大学入学共通テスト(数学) 過去問
令和6年度(2024年度)本試験
問15 (数学Ⅰ・数学A(第2問) 問5)
問題文
<規則>
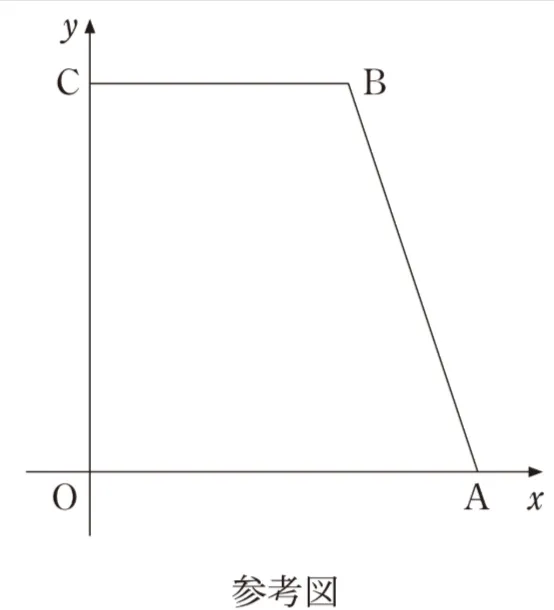
・Pは、Oから出発して毎秒1の一定の速さでx軸上を正の向きにAまで移動し、Aに到達した時点で移動を終了する。
・Qは、Cから出発してy軸上を負の向きにOまで移動し、Oに到達した後はy軸上を正の向きにCまで移動する。そして、Cに到達した時点で移動を終了する。ただし、Qは毎秒2の一定の速さで移動する。
・P、Qは同時刻に移動を開始する。
この規則に従ってP、Qが移動するとき、P、QはそれぞれA、Cに同時刻に到達し、移動を終了する。
以下において、P、Qが移動を開始する時刻を開始時刻、移動を終了する時刻を終了時刻とする。
(3)開始時刻から終了時刻までのΔPBQの面積について、面積の最小値は( オ )であり、最大値は( カキ )である。
( カキ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)本試験 問15(数学Ⅰ・数学A(第2問) 問5) (訂正依頼・報告はこちら)
<規則>
・Pは、Oから出発して毎秒1の一定の速さでx軸上を正の向きにAまで移動し、Aに到達した時点で移動を終了する。
・Qは、Cから出発してy軸上を負の向きにOまで移動し、Oに到達した後はy軸上を正の向きにCまで移動する。そして、Cに到達した時点で移動を終了する。ただし、Qは毎秒2の一定の速さで移動する。
・P、Qは同時刻に移動を開始する。
この規則に従ってP、Qが移動するとき、P、QはそれぞれA、Cに同時刻に到達し、移動を終了する。
以下において、P、Qが移動を開始する時刻を開始時刻、移動を終了する時刻を終了時刻とする。
(3)開始時刻から終了時刻までのΔPBQの面積について、面積の最小値は( オ )であり、最大値は( カキ )である。
( カキ )にあてはまるものを1つ選べ。

- 11
- 12
- 13
- 14
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
PとQはそれぞれ直線上を一定速度で移動し、両者とも同時に始点から終点へ到達します。
「ΔPBQの面積」は、時間tにおけるP(t)BQ(t)という三角形の面積です。
この面積を時間で表して最小値を求めれば答えが得られます。
この解説ではベクトルOAをOA→と表現します。
PはO(0,0)からA(6,0)へx軸上を速度1で移動し停止するので0≤t≤6です。
QはC(0,6)からy軸上を下方向に速度2でOへ、そこから再び上方向にCへ移動するので0≤t≤6です。
PはO(0,0)からA(6,0)へx軸上を速度1で移動するので時刻tでの点Pの座標P(t)は
P(t)=(t,0)(0≤t≤6)
QはC(0,6)からy軸上を下方向に速度2でOへ、そこから再び上方向にCへ移動します。
つまり時刻tでの点Qの座標Q(t)は
Q(t)=(0,6−2t)(0≤t≤3)
Q(t)=(0,2t−6)(3<t≤6)
三角形の頂点を P、B、Q、点Qの座標をQyとします。
PB→=B−P=(4−t,6)(0≤t≤6)
PQ→=B−Q=(−t,Qy)
2次元空間でベクトル (a,b)と (c,d)の平行四辺形の面積は|ad−bc|で求められ、対角線で2分された三角形の面積はその半分です。
時刻tにおける三角形PBQの面積をS(t)とすると
S(t)
=(1/2)*|(4-t)(Qy)+6t|
(i)0≤t≤3
この時Qy=6−2tです。
S(t)
=(1/2)*|(4-t)(6−2t)+6t|
=(1/2)*|2t2−8t+24|
ここで0≤t≤3で2t2−8t+24>0なので、
S(t)
=t2−4t+12
=(t-2)2+8
S(t)は下に凸のtに関する二次関数であり、t=2が極値となるためt=0で最大値12をとります。
(ii)3<t≤6
この時Qy=2t-6です。
S(t)
=(1/2)*|(4-t)(2t-6)+6t|
=(1/2)*|-2t2+20t-24|
ここで3<t≤6で-2t2+20t-24>0なので、
S(t)
=-t2+10t-12
=-(t-5)2+13
S(t)上に凸のtに関する二次関数のため、t=5で最小値13をとります。
(i)(ii)よりS(t)の最小値は13です。
参考になった数0
この解説の修正を提案する
前の問題(問14)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問16)へ