大学入学共通テスト（数学） 過去問
令和6年度（2024年度）本試験
問27 (数学Ⅰ・数学A（第3問） 問4)
問題文
箱の中にカードが2枚以上入っており、それぞれのカードにはアルファベットが1文字だけ書かれている。この箱の中からカードを1枚取り出し、書かれているアルファベットを確認してからもとに戻すという試行を繰り返し行う。
（1）箱の中に［A］、［B］のカードが1枚ずつ全部で2枚入っている場合を考える。
以下では、2以上の自然数nに対し、n回の試行でA、Bがそろっているとは、n回の試行で［A］、［B］のそれぞれが少なくとも1回は取り出されることを意味する。
（ⅲ）4回の試行でA、Bがそろっている取り出し方は（ エオ ）通りある。よって、4回の試行でA、Bがそろっている確率は（ カ ）／（ キ ）である。
（ カ ）／（ キ ）にあてはまるものを1つ選べ。
（1）箱の中に［A］、［B］のカードが1枚ずつ全部で2枚入っている場合を考える。
以下では、2以上の自然数nに対し、n回の試行でA、Bがそろっているとは、n回の試行で［A］、［B］のそれぞれが少なくとも1回は取り出されることを意味する。
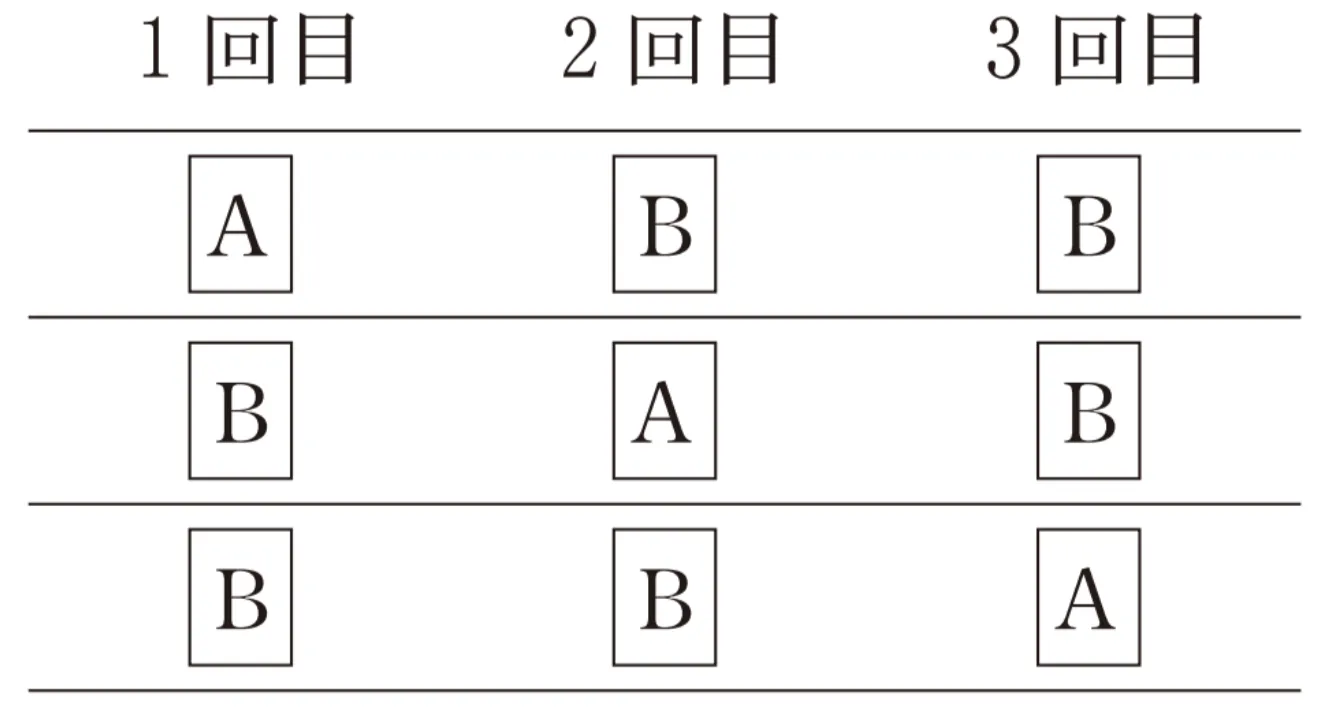
（ⅲ）4回の試行でA、Bがそろっている取り出し方は（ エオ ）通りある。よって、4回の試行でA、Bがそろっている確率は（ カ ）／（ キ ）である。
（ カ ）／（ キ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（数学）試験 令和6年度（2024年度）本試験 問27（数学Ⅰ・数学A（第3問） 問4） （訂正依頼・報告はこちら）
箱の中にカードが2枚以上入っており、それぞれのカードにはアルファベットが1文字だけ書かれている。この箱の中からカードを1枚取り出し、書かれているアルファベットを確認してからもとに戻すという試行を繰り返し行う。
（1）箱の中に［A］、［B］のカードが1枚ずつ全部で2枚入っている場合を考える。
以下では、2以上の自然数nに対し、n回の試行でA、Bがそろっているとは、n回の試行で［A］、［B］のそれぞれが少なくとも1回は取り出されることを意味する。
（ⅲ）4回の試行でA、Bがそろっている取り出し方は（ エオ ）通りある。よって、4回の試行でA、Bがそろっている確率は（ カ ）／（ キ ）である。
（ カ ）／（ キ ）にあてはまるものを1つ選べ。
（1）箱の中に［A］、［B］のカードが1枚ずつ全部で2枚入っている場合を考える。
以下では、2以上の自然数nに対し、n回の試行でA、Bがそろっているとは、n回の試行で［A］、［B］のそれぞれが少なくとも1回は取り出されることを意味する。
（ⅲ）4回の試行でA、Bがそろっている取り出し方は（ エオ ）通りある。よって、4回の試行でA、Bがそろっている確率は（ カ ）／（ キ ）である。
（ カ ）／（ キ ）にあてはまるものを1つ選べ。
- 5／7
- 1／6
- 7／8
- 3／9
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
確率は、「（条件にあてはまる場合の数）/（起こりうる全ての場合の数）」で計算できます。
4回の試行でA、Bがそろっている取り出し方を求めます。
1回の試行につき、出るカードは［A］か［B］の2通りです。
これを4回繰り返すので、取り出し方の総数は、
24=16通り
となります。
次に、問題の条件である「A、Bがそろっている」の反対、つまり「A、Bがそろっていない」場合を考えます。
これは「AAAA」と「BBBB」の2通りだけです。
したがって、「A、Bがそろっていない」場合の数は、1+1=2通りとなります。
求めたいのは「A、Bがそろっている」場合の数なので、全体の16通りから「そろっていない」2通りを引けば4回の試行でA、Bがそろっている取り出し方を求めることができます。
16-2=14通り
したがって、求める確率は、
14/16=7/8
参考になった数0
この解説の修正を提案する
前の問題（問26）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問28）へ