大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問7 (数学Ⅰ・数学A(第1問) 問7)
問題文
地点Aと地点Bが一般道路[あ](以下、道路[あ])と高速道路[い](以下、道路[い])でつながっている。車の制限速度は、道路[あ]が時速30kmで、道路[い]が時速80kmである。道路[あ]におけるAからBまでの道のりは75kmであり、道路[い]におけるAからBまでの道のりは48kmである。
道路[あ]上に地点Pがあり、道路[あ]におけるPからAまでの道のりは10kmである。また、地点Qは道路[あ]においてPとBの間にある。ただし、Qは、P、Bのいずれとも異なる地点である。
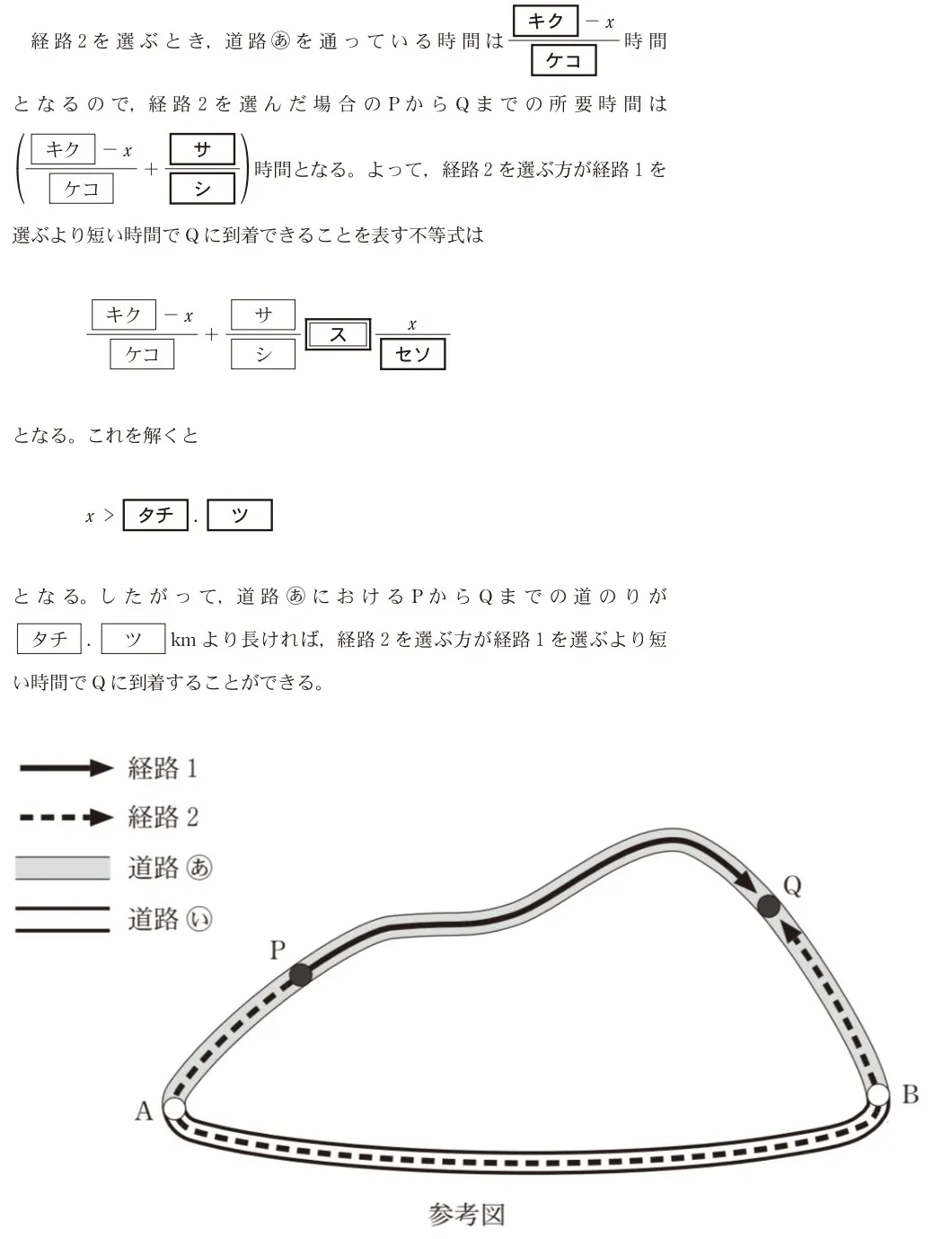
太郎さんは、PからQに車で行くことになった。PからQに行くには、Pから道路[あ]だけを通ってQに行く経路1と、Pから道路[あ]を通ってAに行き、Aから道路[い]を通ってBに行き、Bから道路[あ]を通ってQに行く経路2がある。
道路[あ]におけるPからQまでの道のりがどれくらいであれば、経路2を選ぶ方が経路1を選ぶより短い時間でQに到着できるかを考えたい。ただし、車はつねに制限速度で走るものとする。
道路[あ]において、PからQまでの道のりをxkmとすると、PからAまでの道のりが10kmであり、PとBの間にQがあることからx<65である。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問7(数学Ⅰ・数学A(第1問) 問7) (訂正依頼・報告はこちら)
地点Aと地点Bが一般道路[あ](以下、道路[あ])と高速道路[い](以下、道路[い])でつながっている。車の制限速度は、道路[あ]が時速30kmで、道路[い]が時速80kmである。道路[あ]におけるAからBまでの道のりは75kmであり、道路[い]におけるAからBまでの道のりは48kmである。
道路[あ]上に地点Pがあり、道路[あ]におけるPからAまでの道のりは10kmである。また、地点Qは道路[あ]においてPとBの間にある。ただし、Qは、P、Bのいずれとも異なる地点である。
太郎さんは、PからQに車で行くことになった。PからQに行くには、Pから道路[あ]だけを通ってQに行く経路1と、Pから道路[あ]を通ってAに行き、Aから道路[い]を通ってBに行き、Bから道路[あ]を通ってQに行く経路2がある。
道路[あ]におけるPからQまでの道のりがどれくらいであれば、経路2を選ぶ方が経路1を選ぶより短い時間でQに到着できるかを考えたい。ただし、車はつねに制限速度で走るものとする。
道路[あ]において、PからQまでの道のりをxkmとすると、PからAまでの道のりが10kmであり、PとBの間にQがあることからx<65である。

- タチ:43 ツ:2
- タチ:44 ツ:3
- タチ:45 ツ:4
- タチ:46 ツ:5
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答 タチ:46 ツ:5
解説
解くべき不等式は
((75-x)/30)+(3/5)<x/30
です。
両辺に30をかけて
(75-x)+18<x
整理して
93<2x
2x>93
x>46.5
よって答えは「タチ:46 ツ:5」となります。
補足
直前の問題の解説を一部再掲しておきます。
参考になった数0
この解説の修正を提案する
前の問題(問6)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問8)へ