大学入学共通テスト(数学) 過去問
令和6年度(2024年度)追・試験
問24 (数学Ⅰ・数学A(第2問) 問10)
問題文
演技などの採点において、複数の審査員による採点結果の評点のうち、最小値と最大値をそれぞれ1個ずつ除外した評点によって評価が行われることがある。
以下では、審査員がそれぞれ1,2,3,4,5のいずれかの評点をつけるものとする。

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(数学)試験 令和6年度(2024年度)追・試験 問24(数学Ⅰ・数学A(第2問) 問10) (訂正依頼・報告はこちら)
演技などの採点において、複数の審査員による採点結果の評点のうち、最小値と最大値をそれぞれ1個ずつ除外した評点によって評価が行われることがある。
以下では、審査員がそれぞれ1,2,3,4,5のいずれかの評点をつけるものとする。

正解!素晴らしいです
残念...

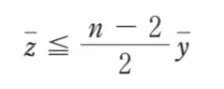
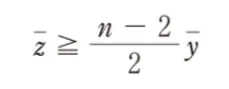
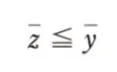
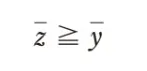
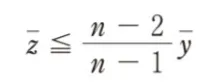
この過去問の解説 (1件)
01
解答 チ:「z ≦ y」
解説
問題文ではx,y,zの上にバー(横棒)がついていますが、
解説文では単にx,y,zと書くことにします。
前問で、「ソ:2/n タ:(n−2)/n」であることを求めました。
つまり、
x=(2/n)z + ((n−2)/n)y
です。
「x ≦ y」を同値変形していきます。
x ≦ y
(2/n)z + ((n−2)/n)y ≦ y
2z + (n−2)y ≦ ny (両辺をn倍)
2z ≦ ny−(n−2)y
2z ≦ ny−ny+2y
2z ≦ 2y
z ≦ y
よって答えは「z ≦ y」となります。
補足
以下はソタの解説です(前問の解説から引用)。
この選択肢が正解となります。
参考になった数0
この解説の修正を提案する
前の問題(問23)へ
令和6年度(2024年度)追・試験 問題一覧
次の問題(問25)へ