第三種電気主任技術者（電験三種） 過去問
令和6年度（2024年）下期
問17 (理論 問16（a）)
問題文
図のブリッジ回路を用いて、未知抵抗Rxを測定したい。抵抗R1＝3kΩ、R2＝2kΩ、R4＝3kΩとし、R3＝6kΩの滑り抵抗器の接触子の接点Cをちょうど中央に調整したとき（Rac＝Rbc＝3kΩ）ブリッジが平衡したという。次の問に答えよ。
ただし、直流電圧源は6Vとし、電流計の内部抵抗は無視できるものとする。
未知抵抗Rxの値［kΩ］として、最も近いものを次のうちから一つ選べ。
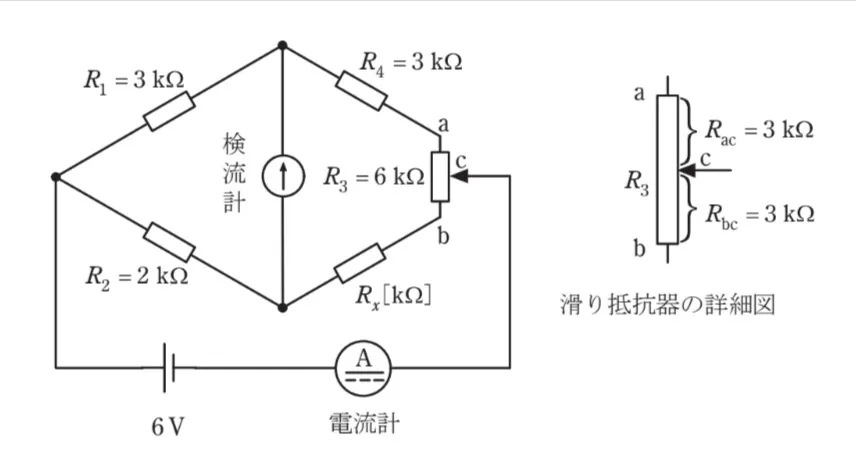
ただし、直流電圧源は6Vとし、電流計の内部抵抗は無視できるものとする。
未知抵抗Rxの値［kΩ］として、最も近いものを次のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
第三種電気主任技術者（電験三種）試験 令和6年度（2024年）下期 問17（理論 問16（a）） （訂正依頼・報告はこちら）
図のブリッジ回路を用いて、未知抵抗Rxを測定したい。抵抗R1＝3kΩ、R2＝2kΩ、R4＝3kΩとし、R3＝6kΩの滑り抵抗器の接触子の接点Cをちょうど中央に調整したとき（Rac＝Rbc＝3kΩ）ブリッジが平衡したという。次の問に答えよ。
ただし、直流電圧源は6Vとし、電流計の内部抵抗は無視できるものとする。
未知抵抗Rxの値［kΩ］として、最も近いものを次のうちから一つ選べ。
ただし、直流電圧源は6Vとし、電流計の内部抵抗は無視できるものとする。
未知抵抗Rxの値［kΩ］として、最も近いものを次のうちから一つ選べ。
- 0.1
- 0.5
- 1
- 1.5
- 2
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
ブリッジの平衡条件を利用して未知の抵抗値をを求める計算問題です。
ブリッジの平衡条件の公式より、
R1(Rx+Rbc)＝R2(R4+Rac)
3✕(Rx+3)＝2✕(3+3)
3Rx+9＝12
3Rx＝12-9
3Rx＝3
Rx＝1[kΩ]
となります。
参考になった数4
この解説の修正を提案する
02
ブリッジ回路を用いて未知の抵抗値を求める問題です。
接点Cが中央に調整した時に、Rac=Rbc=3kΩと平衡になるなることから、R４＝６kΩ、Rｘ＝3+Xとすると
ブリッジ回路の平衡条件から３×（3+X）₌６×２となるように考えられます。
９＋３X＝12
X＝１となります。
誤：計算結果と異なります。
誤：計算結果と異なります。
正：計算結果と合致してこれが正解となります。
誤：計算結果と異なります。
誤：計算結果と異なります。
ブリッジ回路の複雑な回路の未知の抵抗値を求める問題でした。
平衡条件に合わせるように平衡になっていたため、計算しやすい問題でした。
少し見方を変えると見えてくるものでした。
参考になった数0
この解説の修正を提案する
03
ブリッジ回路内の未知の抵抗を求める問題です。
ブリッジ回路の平衡条件より、
R1(Rx+Rbc)=R2(R4+Rac)
3×103(Rx+3×103)=2×103(3×103+3×103)
Rx=1×103=1[kΩ]
と求められます。
参考になった数0
この解説の修正を提案する
前の問題（問16）へ
令和6年度（2024年）下期 問題一覧
次の問題（問18）へ